题目内容
14.(1)如图1,D1是△ABC的边AB上的一点,则图中共有3个三角形;(2)如图2,D1,D2是△ABC的边AB上的两点,则图中共有6个三角形;
(3)如图3,D1,D2,…,D10是△ABC的边AB上的10个点,则图中共有66个三角形.

分析 (1)根据三角形的概念:由不在同一条直线上的三条线段首尾顺次相接所组成的图形叫做三角形进行分析即可.
(2)根据三角形的概念:由不在同一条直线上的三条线段首尾顺次相接所组成的图形叫做三角形进行分析即可.
(3)直线AB上有几条线段就有几个三角形;由线段的计数方法计算即可得出答案.
解答 解:(1)图中三角形有:△ABC、△AD1C、△AD1B共3个;
(2)图中三角形有:△ACD1、△ACD2、△ABC、△D1CD2、△D1CB、△D2CB共6个,
(3)∵直线AB上有12个点,
∴直线AB上的线段共有:$\frac{12(12-1)}{2}$=66(条),
即图中共有66个三角形.
故答案为:3,6,66.
点评 此题主要考查了三角形,关键是在数三角形时,要做到不重不漏.

练习册系列答案
相关题目
9.下列说法正确的是( )
| A. | 三点确定一个圆 | |
| B. | 正多边形既是轴对称图形也是中心对称图形 | |
| C. | 等弧所对的圆周角相等 | |
| D. | 三角形的外心到三边的距离相等 |
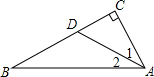 如图,已知∠C=90°,∠1=∠2=30°,若BC=15,则点D到边AB的距离为5.
如图,已知∠C=90°,∠1=∠2=30°,若BC=15,则点D到边AB的距离为5. 如图,AD与BC交于点O,AB∥CD,若AB=4cm,CD=8cm,AD=12cm,求AO的长.
如图,AD与BC交于点O,AB∥CD,若AB=4cm,CD=8cm,AD=12cm,求AO的长. 如图,$\frac{AB}{AD}$=$\frac{FB}{FE}$,AB=8cm,AD=2cm,BC=7.2cm,E是BC的中点,求EF,BF的长.
如图,$\frac{AB}{AD}$=$\frac{FB}{FE}$,AB=8cm,AD=2cm,BC=7.2cm,E是BC的中点,求EF,BF的长. 如图,AB是⊙O的直径,C是⊙O上的一点,∠A=35°,则∠B=55°.
如图,AB是⊙O的直径,C是⊙O上的一点,∠A=35°,则∠B=55°.