题目内容
已知:y关于x的函数y=k2x2-(2k+1)x+1的图象与坐标轴只有两个不同的交点A、B,P点坐标为(4,2),则△PAB的面积为 .
考点:抛物线与x轴的交点
专题:
分析:在y=k2x2-(2k+1)x+1中k可能为0(一次函数y=-x+1),也可能不为0(二次函数y=k2x2-(2k+1)x+1),根据题意,结合一次函数二次函数与坐标轴交点特点,易求点A、B坐标,即能求△PAB的面积.
解答: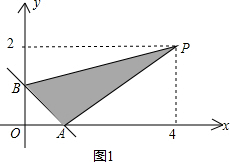 解:当k=0时,y=-x+1,
解:当k=0时,y=-x+1,
设一次函数图象与x轴交于A,与y轴交于B,则A(1,0),B(0,1),
此时,S△PAB=
(1+2)×4-
×1×1-
×3×2=
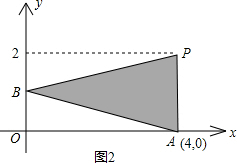
当k≠0时,函数y=k2x2-(2k+1)x+1的图象为抛物线,与y轴交于B(0,1),
∵它的图象与坐标轴只有两个交点,
∴它的图象与x轴只有一个交点,设为A点,
∴△=(2k+1)2-4k2=0,
 解得:k=-
解得:k=-
,
∴抛物线y=
x2-
x+1与x轴交于A(4,0),
∴此时S△PAB=
×2×4=4,
综合得:△PAB的面积为
或4,
故答案为:
或4.
 解:当k=0时,y=-x+1,
解:当k=0时,y=-x+1,设一次函数图象与x轴交于A,与y轴交于B,则A(1,0),B(0,1),
此时,S△PAB=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 5 |
| 2 |
当k≠0时,函数y=k2x2-(2k+1)x+1的图象为抛物线,与y轴交于B(0,1),
∵它的图象与坐标轴只有两个交点,
∴它的图象与x轴只有一个交点,设为A点,
∴△=(2k+1)2-4k2=0,
 解得:k=-
解得:k=-| 1 |
| 4 |
∴抛物线y=
| 1 |
| 16 |
| 1 |
| 2 |
∴此时S△PAB=
| 1 |
| 2 |
综合得:△PAB的面积为
| 5 |
| 2 |
故答案为:
| 5 |
| 2 |
点评:此题难度较大,考查一次函数、二次函数的图象和性质,用到的知识点:求二次函数y=ax2+bx+c(a,b,c是常数,a≠0)与x轴的交点坐标,令y=0,即ax2+bx+c=0,解关于x的一元二次方程即可求得交点横坐标.其中还渗透分类讨论思想,综合性大.

练习册系列答案
相关题目
已知一个圆锥形零件的母线长为5,底面半径为2,则这个圆锥形零件的侧面积为( )
| A、5π | B、10π | C、3π | D、6π |

 如图,点C,D两点在以AB为直径的⊙O上,AD∥OC,∠BOC=110°,则∠AOD=
如图,点C,D两点在以AB为直径的⊙O上,AD∥OC,∠BOC=110°,则∠AOD=