题目内容
2．满足（2-m）m2-m-2=1的所有实数m的和为（ ）| A． | 2 | B． | 3 | C． | 4 | D． | 5 |
分析 根据（-1）的偶数次幂等于，可得m的值，根据非零的零次幂等于1，可得m的值，根据1的任何次幂都等于1，可得答案．
解答 解：当2-m=-1时，m=3，m2-m-2=9-3-2=4，即（-1）4=1，
当2-m≠0时，m2-m-2=0，解得m=-1，即（2-m）${\;}^{{m}^{2}-m-2}$=30=1，
当2-m=1时，m=1，m2-m-2=1-1-2=-2，即1-2=1，
3+（-1）+1=3．
故选：B．
点评 本题考查了零指数幂，利用非零的零次幂等于1，-1的偶数次幂等于1，1的任何数次幂等于是解题关键，以防遗漏．
练习册系列答案
相关题目
13．
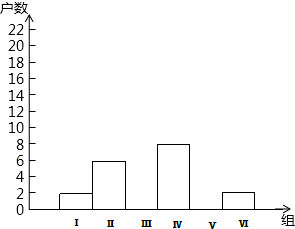今年是我国施行“清明”小长假的第二年，在长假期间，某校团委要求学生参加一项社会调查活动．九年级学生小青想了解她所居住的小区500户居民的家庭人均收入情况，从中随机调查了40户居民家庭的人均收入情况（收入取整数，单位：元）并绘制了如下的分布表和分布图：
根据以上提供的信息，解答下列问题：
（1）补全分布表、分布图；
（2）这40户家庭收入的中位数落在哪一个小组？
（3）被调查的家庭中，参加“清明扫墓“活动的家庭统计如表：
问：估计该小区共有多少户家庭参加了扫墓活动．
今年是我国施行“清明”小长假的第二年，在长假期间，某校团委要求学生参加一项社会调查活动．九年级学生小青想了解她所居住的小区500户居民的家庭人均收入情况，从中随机调查了40户居民家庭的人均收入情况（收入取整数，单位：元）并绘制了如下的分布表和分布图：| 分组 | 户数 | 百分比 |
| Ⅰ：600-799 | 2 | 0.05 |
| Ⅱ：800-999 | 6 | 0.15 |
| Ⅲ：1000-1199 | 0.45 | |
| Ⅳ：1200-1399 | 8 | 0.20 |
| Ⅴ：1400-1599 | ||
| Ⅵ：1600-1800 | 2 | 0.05 |
| 合计 | 40 | 1.00 |
（1）补全分布表、分布图；
（2）这40户家庭收入的中位数落在哪一个小组？
（3）被调查的家庭中，参加“清明扫墓“活动的家庭统计如表：
| 收入情况 | 600-799 | 800-999 | 1000-1199 | 1200-1399 | 1400-1599 | 1600-1800 |
| $\frac{参加扫墓家庭数}{被调查家庭数}$ | $\frac{1}{2}$ | $\frac{1}{3}$ | $\frac{1}{6}$ | $\frac{1}{4}$ | 1 | 1 |
14．下列等式变形正确的是（ ）
| A． | 如果s=ab，那么b=$\frac{s}{a}$ | B． | 如果x=6，那么x=3 | ||
| C． | 如果x-3=y-3，那么x-y=0 | D． | 如果mx=my，那么x=y |