已知关于x的方程x2-2x+3k=0没有实数根.则k的取值范围是k＞$\frac{1}{3}$．题目和参考答案——青夏教育精英家教网—

题目内容

16．已知关于x的方程x²-2x+3k=0没有实数根，则k的取值范围是k＞$\frac{1}{3}$．

分析由方程没有实数根结合根的判别式，可得出关于k的一元一次不等式，解不等式即可得出结论．

解答解：∵关于x的方程x²-2x+3k=0没有实数根，
∴△=（-2）²-4×1×3k=4-12k＜0，
解得：k＞$\frac{1}{3}$．
故答案为：k＞$\frac{1}{3}$．

点评本题考查了根的判别式以及解一元一次不等式，解题的关键是得出△=4-12k＜0．本题属于基础题，难度不大，解决该题型题目时，根据方程根的情况结合根的判别式，得出不等式（或不等式组）是关键．

练习册系列答案

相关题目

6．

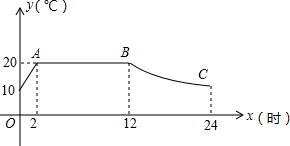我市某蔬菜生产基地用装有恒温系统的大棚栽培一种适宜生长温度为15-20℃的新品种，如图是某天恒温系统从开启到关闭及关闭后，大棚里温度y（℃）随时间x（h）变化的函数图象，其中AB段是恒温阶段，BC段是双曲线y=$\frac{k}{x}$的一部分，请根据图中信息解答下列问题：
（1）求k的值；
（2）恒温系统在一天内保持大棚里温度在15℃及15℃以上的时间有多少小时？

7．如图1，AB为半圆O的直径，D为BA的延长线上一点，DC为半圆O的切线，切点为C．
（1）求证：∠ACD=∠B；
（2）如图2，∠BDC的平分线分别交AC，BC于点E，F；
①求tan∠CFE的值；
②若AC=3，BC=4，求CE的长．

4．

如图，把一张长方形纸片折叠，如果∠2=64°，那么∠1=58°．

11．若△ABC≌△A′B′C′，且AB=AC=9，△ABC的周长为26cm，则B′C′的长为（　　）

1．已知点（-4，y₁），（2，y₂）都在直线y=-2x+3上，则y₁，y₂大小关系是（　　）

y₁＞y₂

y₁=y₂

y₁＜y₂

8．命题“全等三角形的周长相等”的逆命题是周长相等的三角形是全等三角形．

5．已知xy＞0，化简二次根式$x\sqrt{-\frac{y}{x^2}}$的正确结果是（　　）

6．在三角形纸片ABC中，∠C=90°，∠B=30°，点D（不与B，C重合）是BC上任意一点，将此三角形纸片按下列方式折叠，若EF的长度为a，则△DEF的周长为3a（用含a的式子表示）．

试题分类