题目内容
5.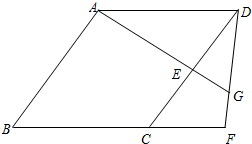 已知:如图,四边形ABCD是菱形,点E在边CD上,点F在BC的延长线上,CF=DE,AE的延长线与DF相交于点G.
已知:如图,四边形ABCD是菱形,点E在边CD上,点F在BC的延长线上,CF=DE,AE的延长线与DF相交于点G.(1)求证:∠CDF=∠DAE;
(2)如果DE=CE,求证:AE=3EG.
分析 (1)由四边形ABCD是菱形,得到AD=CD,AD∥BC,根据平行线的性质得到∠ADE=∠DCF,推出△ADE≌△DCF,根据全等三角形的性质得到∠CDF=∠DAE;
(2)过E作EH∥BF交DF于H,根据三角形中位线的性质得到EH=$\frac{1}{2}$CF,推出DE=CF=$\frac{1}{2}$CD=$\frac{1}{2}$AD,求得EH=$\frac{1}{4}$AD,根据相似三角形的性质即可得到结论.
解答 解:∵四边形ABCD是菱形,
∴AD=CD,AD∥BC,
∴∠ADE=∠DCF,
在△ADE与△DCF中,
$\left\{\begin{array}{l}{AD=CD}\\{∠ADE=∠DCE}\\{DE=CF}\end{array}\right.$,
∴△ADE≌△DCF,
∴∠CDF=∠DAE;
(2)过E作EH∥BF交DF于H,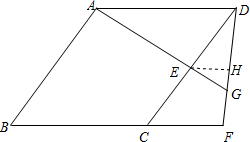 ∵DE=CE,
∵DE=CE,
∴EH=$\frac{1}{2}$CF,
∵△ADE≌△DCF,
∴DE=CF=$\frac{1}{2}$CD=$\frac{1}{2}$AD,
∴EH=$\frac{1}{4}$AD,
∵EH∥AD,
∴△GHE∽△GDA,
∴$\frac{GE}{GA}=\frac{EH}{AD}=\frac{1}{4}$,
∴AE=3EG.
点评 本题考查了相似三角形的判定和性质,菱形的性质,全等三角形的判定与和性质,三角形的中位线的性质,掌握的周长辅助线是解题的关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
16.下列各式是最简二次根式的是( )
| A. | $\sqrt{32}$ | B. | $\sqrt{\frac{8}{9}}$ | C. | $\sqrt{15}$ | D. | $\frac{1}{\sqrt{2}}$ |
10.如图,是由一些小立方块所搭几何体的三种视图,若在所搭几何体的基础上(不改变原几何体中小立方块的位置),继续添加相同的小立方块,以搭成一个大正方体,至少还需要( )个小立方块.
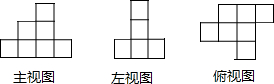

| A. | 36 | B. | 52 | C. | 54 | D. | 55 |
17.小颖对青岛地区6、7月份天气连续十天每天的最高气温进行统计,依次得到以下一组数据:24,25,26,24,26,27,27,26,27,27(单位℃).则这组数据的中位数和众数分别是( )
| A. | 27,26 | B. | 27,26.5 | C. | 26.5,27 | D. | 26,27 |
15.如果点K、L、M、N分别是四边形ABCD的四条边AB、BC、CD、DA的中点,且四边形KLMN是菱形,那么下列选项正确的是( )
| A. | AB⊥BC | B. | AC⊥BD | C. | AB=BC | D. | AC=BD |
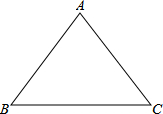 已知△ABC中,AB=AC=5,BC=6(如图所示),将△ABC沿射线BC方向平移m个单位得到△DEF,顶点A、B、C分别与D、E、F对应.若以点A、D、E为顶点的三角形是等腰三角形,且AE为腰,则m的值是6或$\frac{25}{6}$.
已知△ABC中,AB=AC=5,BC=6(如图所示),将△ABC沿射线BC方向平移m个单位得到△DEF,顶点A、B、C分别与D、E、F对应.若以点A、D、E为顶点的三角形是等腰三角形,且AE为腰,则m的值是6或$\frac{25}{6}$.