题目内容
15.阅读理解(1)观察一列数a1=3,a2=9,a3=27,a4=81…,发现从第二项开始,每一项与前一项之比是一个常数,这个常数是3;根据此规律,如果an(n为正整数)表示这个数列的第n项,那么a6=36,an=3n;(可用幂的形式表示)
(2)如果想要求1+2+22+23+…+29的值,可令S=1+2+22+23+…+29①,将①式两边同乘以2,得2S=2+22+23+24+…+210②,由②减去①式,得S=$\frac{{5}^{10}-5}{4}$.
(3)利用(2)的方法,求1+5+52+53+…+59.
分析 (1)寻找规律即可解决问题.
(2)利用等式的性质构造两个等式,S=1+2+22+23+…+29①,2S=2+22+23+24+…+210②,②-①即可解决问题.
(3)解法类似(2).
解答 解:(1)∵a1=3,a2=9=32,a3=27=33,a4=81=34,
∴每一项与前一项之比是3,a6=36,an=3n,
故答案分别为3,36,3n.
(2)∵S=1+2+22+23+…+29 ①,
2S=2+22+23+24+…+210 ②,
②-①得S=210-1,
故答案为210-1.
(3)设S=1+5+52+53+…+59 ①,
5S=5+52+53+54+…+510 ②
②-①得4S=510-5,
∴S=$\frac{{5}^{10}-5}{4}$.
故答案为$\frac{{5}^{10}-5}{4}$.
点评 本题考查规律题、学会利用等式的性质,构造两个等式,再利用解方程组的思想解决问题是解题的关键,属于中考常考题型.

练习册系列答案
 名校通行证有效作业系列答案
名校通行证有效作业系列答案
相关题目
5.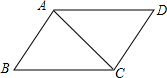 如图,AB=CD,AB∥CD,判定△ABC≌△CDA的依据是( )
如图,AB=CD,AB∥CD,判定△ABC≌△CDA的依据是( )
 如图,AB=CD,AB∥CD,判定△ABC≌△CDA的依据是( )
如图,AB=CD,AB∥CD,判定△ABC≌△CDA的依据是( )| A. | SSS | B. | SAS | C. | ASA | D. | HL |
3.如果x<0,那么x的立方根是( )
| A. | $\root{3}{x}$ | B. | $\sqrt{-x}$ | C. | -$\sqrt{x}$ | D. | ±$\root{3}{x}$ |
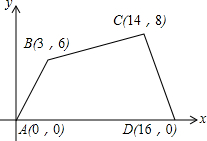 如图所示的直角坐标系中,四边形ABCD各个顶点的坐标分别是A(0,0),B(3,6),C(14,8),D(16,0),
如图所示的直角坐标系中,四边形ABCD各个顶点的坐标分别是A(0,0),B(3,6),C(14,8),D(16,0),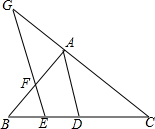 如图,AD平分∠BAC,∠BFE=∠G,∠B-∠G=20°,∠ADC=100°.
如图,AD平分∠BAC,∠BFE=∠G,∠B-∠G=20°,∠ADC=100°.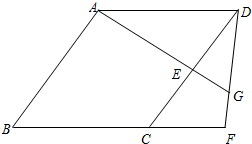 已知:如图,四边形ABCD是菱形,点E在边CD上,点F在BC的延长线上,CF=DE,AE的延长线与DF相交于点G.
已知:如图,四边形ABCD是菱形,点E在边CD上,点F在BC的延长线上,CF=DE,AE的延长线与DF相交于点G.