题目内容
5．
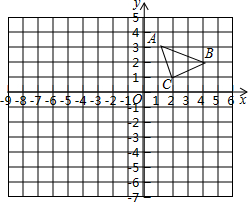如图，△ABC的顶点坐标分别为A（1，3）、B（4，2）、C（2，1）．（1）作出与△ABC关于x轴对称的△A 1B1C1，并写出点A1的坐标；
（2）以原点O 为位似中心，在原点的另一侧画出△A2B2C2，使$\frac{AB}{{A}_{2}{B}_{2}}$=$\frac{1}{2}$，并写出点A2的坐标．
分析 （1）利用关于x轴对称的点的坐标特征，写出A1、B1、C1的坐标，然后描点即可得到△A 1B1C1；
（2）把A、B、C的横纵坐标后乘以-2得到出A2、B2、C2的坐标，然后描点即可得到△A 2B2C2．
解答 解：（1）如图，△A 1B1C1为所作，A1（1，-3）；
（2）如图，△A2B2C2为所作，A2（-2，-6）．
点评 本题考查了位似变换：如果两个图形不仅是相似图形，而且对应顶点的连线相交于一点，对应边互相平行，那么这样的两个图形叫做位似图形，这个点叫做位似中心．
练习册系列答案
相关题目
15．一项工程，甲单独做需10天完成，乙单独做需6天完成，现由甲先做2天，乙再加入合作，设完成这项工程共需x天，由题意可列方程（ ）
| A． | $\frac{x}{10}$+$\frac{x}{6}$=1 | B． | $\frac{x+2}{10}$+$\frac{x-2}{6}$=1 | C． | $\frac{x}{10}$+$\frac{x-2}{6}$=1 | D． | $\frac{2}{6}$+$\frac{x-2}{10}$+$\frac{x-2}{6}$=1 |
16．已知关于x的一元二次方程：x2-6x+k-1=0有两个相等的实根，则k=（ ）
| A． | -8 | B． | 9 | C． | 10 | D． | -10 |
13．下列各式中计算结果为9的是（ ）
| A． | （-2）+（-7） | B． | -32 | C． | （-3）2 | D． | 3×3-1 |
20．下列各数中，相反数是-2的是（ ）
| A． | -$\frac{1}{2}$ | B． | $\frac{1}{2}$ | C． | -2 | D． | 2 |
在“文博会”期间，某公司展销如图所示的长方形工艺品，该工艺品长60cm，宽40cm，中间镶有宽度相同的三条丝绸花边．