题目内容
17.已知:抛物线y=x2+$\frac{1}{4}$m与直线y=x有两个不同的交点,两个交点的横坐标分别是a,b,则m的取值范围是m<1,若n=ab-2b2+2b+1,则n的取值范围是n<$\frac{7}{4}$.分析 根据抛物线y=x2+$\frac{1}{4}$m与直线y=x有两个不同的交点,则方程x2+$\frac{1}{4}$m=x中的△>0,解出可得m的取值;由根与系数的关系得:a+b=1,ab=$\frac{1}{4}$m,把n=ab-2b2+2b+1变形后,得:3m=4n-4,求出n的取值.
解答 解:x2+$\frac{1}{4}$m=x,
x2-x+$\frac{1}{4}$m=0,
△=(-1)2-4×1×$\frac{1}{4}$m=1-m>0,
∴m<1,
∵两个交点的横坐标分别是a,b,
∴a+b=1,ab=$\frac{1}{4}$m,
∴a=1-b,
∴n=ab-2b2+2b+1,
=b(a-2b)+2b+1,
=b(1-b-2b)+2b+1,
=b-3b2+2b+1,
=3b-3b2+1,
=-3b(b-1)+1,
=3ab+1,
=$\frac{3}{4}$m+1,
3m=4n-4
m=$\frac{4n-4}{3}$<1,
∴n<$\frac{7}{4}$,
故答案为:m<1;n<$\frac{7}{4}$.
点评 本题考查了根与系数的关系、二次函数的性质.将根与系数的关系与代数式变形相结合解题是一种经常使用的解题方法.

练习册系列答案
 同步练习强化拓展系列答案
同步练习强化拓展系列答案
相关题目
2. 如图,在△ABC中,∠B=63°,∠C=51°,AE是∠BAC的平分线,则∠BEA的度数为( )
如图,在△ABC中,∠B=63°,∠C=51°,AE是∠BAC的平分线,则∠BEA的度数为( )
 如图,在△ABC中,∠B=63°,∠C=51°,AE是∠BAC的平分线,则∠BEA的度数为( )
如图,在△ABC中,∠B=63°,∠C=51°,AE是∠BAC的平分线,则∠BEA的度数为( )| A. | 96° | B. | 84° | C. | 66° | D. | 33° |
7.关于$\sqrt{8}$的叙述错误的是( )
| A. | $\sqrt{8}$=2$\sqrt{2}$ | B. | 面积为8的正方形边长为$\sqrt{8}$ | ||
| C. | 在数轴上可以找到表示$\sqrt{8}$的点 | D. | $\sqrt{8}$是有理数 |
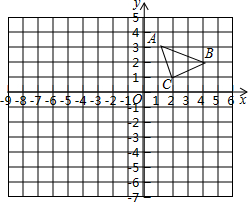 如图,△ABC的顶点坐标分别为A(1,3)、B(4,2)、C(2,1).
如图,△ABC的顶点坐标分别为A(1,3)、B(4,2)、C(2,1). 如图,△ABC中,CD是AB边上的高,AC=8,∠ACD=30°,tan∠ACB=$\frac{5\sqrt{3}}{3}$,点P为CD上一动点,当BP+$\frac{1}{2}$CP最小时,DP=5$\sqrt{3}$.
如图,△ABC中,CD是AB边上的高,AC=8,∠ACD=30°,tan∠ACB=$\frac{5\sqrt{3}}{3}$,点P为CD上一动点,当BP+$\frac{1}{2}$CP最小时,DP=5$\sqrt{3}$.