题目内容
10. 在“文博会”期间,某公司展销如图所示的长方形工艺品,该工艺品长60cm,宽40cm,中间镶有宽度相同的三条丝绸花边.
在“文博会”期间,某公司展销如图所示的长方形工艺品,该工艺品长60cm,宽40cm,中间镶有宽度相同的三条丝绸花边.(1)若丝绸花边的面积为650cm2,求丝绸花边的宽度;
(2)已知该工艺品的成本是40元/件,如果以单价100元/件销售,那么每天可售出200件,另每天除工艺品的成本外所需支付的各种费用是2000元,根据销售经验,如果将销售单价降低1元,每天可多售出20件,请问该公司每天所获利润能否达到22500元,如果能应该把销售单价定为多少元?如果不能,请说明理由.
分析 (1)设出花边的宽,然后表示出花边的长,利用面积公式表示出其面积即可列出方程求解;
(2)先根据题意设每件工艺品降价为x元出售,获利y元,则降价x元后可卖出的总件数为(200+20x),每件获得的利润为(100-x-40),此时根据获得的利润=卖出的总件数×每件工艺品获得的利润,列出二次方程,求解即可.
解答 解:(1)设花边的宽度为xcm,根据题意得:
(60-2x)(40-x)=60×40-650,或60x+80x-2x2=650
解得:x=5或x=65(舍去).
答:丝绸花边的宽度为5cm;
(2)设每件工艺品降价x元出售,则根据题意可得:
(100-x-40)(200+20x)-2000=22500,
整理得:x2-50x+625=0
解这个方程得:x=25
答:当售价100-25=75元时能达到利润22500元.
点评 此题考查了一元二次方程的应用,解题的关键是从实际问题中抽象出一元二次方程模型,难度不大.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
20. 如图所示,小明家在A处,体育馆在B处,星期六小明由家去体育馆打篮球,他想尽快到达体育馆,请你帮助他选择一条最近的路线,应是( )
如图所示,小明家在A处,体育馆在B处,星期六小明由家去体育馆打篮球,他想尽快到达体育馆,请你帮助他选择一条最近的路线,应是( )
 如图所示,小明家在A处,体育馆在B处,星期六小明由家去体育馆打篮球,他想尽快到达体育馆,请你帮助他选择一条最近的路线,应是( )
如图所示,小明家在A处,体育馆在B处,星期六小明由家去体育馆打篮球,他想尽快到达体育馆,请你帮助他选择一条最近的路线,应是( )| A. | A→C→E→B | B. | A→C→D→B | C. | A→C→G→B | D. | A→C→F→E→B |
1.将下列长度的三根木棒首尾顺次连接,不能组成直角三角形的是( )
| A. | 8、15、17 | B. | 7、24、25 | C. | 3、4、5 | D. | 2、3、4 |
18.一位批发商从某服装制造公司购进60包型号为L的衬衫,由于包装工人疏忽,在包裹中混进了型号为M的衬衫,每包混入的M号衬衫数及相应的包数如表所示.
一位零售商从60包中任意选取一包,则包中混入M号衬衫数不超过3的概率是( )
| M号衬衫数 | 1 | 3 | 4 | 5 | 7 |
| 包数 | 20 | 7 | 10 | 11 | 12 |
| A. | $\frac{1}{20}$ | B. | $\frac{1}{15}$ | C. | $\frac{9}{20}$ | D. | $\frac{4}{27}$ |
2. 如图,在△ABC中,∠B=63°,∠C=51°,AE是∠BAC的平分线,则∠BEA的度数为( )
如图,在△ABC中,∠B=63°,∠C=51°,AE是∠BAC的平分线,则∠BEA的度数为( )
 如图,在△ABC中,∠B=63°,∠C=51°,AE是∠BAC的平分线,则∠BEA的度数为( )
如图,在△ABC中,∠B=63°,∠C=51°,AE是∠BAC的平分线,则∠BEA的度数为( )| A. | 96° | B. | 84° | C. | 66° | D. | 33° |
19.成都市简阳新机场建成后,将成为继北京、上海之后,国内第三个拥有双机场的城市,按照远期规划,新机场将新建的每个航站楼的总面积约为32万平方米,用科学记数法表示32万为( )平方米.
| A. | 0.32×107 | B. | 3.2×106 | C. | 3.2×105 | D. | 3.2×10 |
20.近年来,我国持续大面积的雾霾天气让环保和健康问题成为焦点,为进一步普及环保和健康知识,我市某校举行了“建设宜居扬州,关注环境保护”的知识竞赛,某班学生的成绩统计如下:
则该班学生成绩的中位数是80.
| 成绩(分) | 60 | 70 | 80 | 90 | 100 |
| 人数 | 4 | 8 | 12 | 11 | 5 |
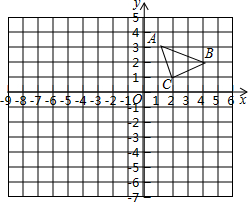 如图,△ABC的顶点坐标分别为A(1,3)、B(4,2)、C(2,1).
如图,△ABC的顶点坐标分别为A(1,3)、B(4,2)、C(2,1).