题目内容
18.已知抛物线y=$\frac{1}{8}$x2-$\frac{1}{4}$x-1与x轴交于A、B两点(点A在点B的左侧)与y轴交于点C(1)求抛物线与坐标轴的交点坐标;
(2)求△ABC外接圆的圆心Q的坐标;
(3)在抛物线的对称轴上一定存在点P,使得∠APB=∠ACB,直接写出点P的坐标.
分析 (1)令x=0得y=-1,从而得到点C的坐标,令y=0得:$\frac{1}{8}$x2-$\frac{1}{4}$x-1=0,求得方程的解,从而得到点A与点B的坐标;
(2)过AB的中点,作直线l⊥AB,则点Q在直线l上.设点Q的坐标为(1,a).因为QA=QC依据两点间的距离公式列出关于a的方程可求得a的值,从而的点点Q的坐标;
(3)作△ABC的外接圆Q.过圆心Q作QD⊥AB交圆Q与点P,作点P关于x轴的对称点P′.由圆周角定理可知∠ACB=∠APB,接下来依据勾股定理可求得AQ的长,由点Q的坐标以及QP的长可求得点P的坐标,依据关于x轴对称的点的坐标特点可求得点P′的坐标.
解答 解:(1)∵令x=0得y=-1,
∴C(0,-1).
∵令y=0得:$\frac{1}{8}$x2-$\frac{1}{4}$x-1=0,整理得:x2-2x-8=0,解得x=4或x=-2,
∴A(-2,0)、B(4,0).
(2)如图1所示:过AB的中点,作直线l⊥AB,则点Q在直线l上.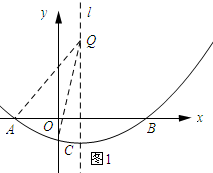
∵A(-2,0)、B(4,0),
∴点Q的横坐标为1.
设点Q的坐标为(1,a).
∵Q是△ABC的外接圆的圆心,
∴QA=QC.
∴$\sqrt{{3}^{2}+{a}^{2}}$=$\sqrt{{1}^{2}+(a+1)^{2}}$,解得:a=3.5.
∴点Q的坐标为(1,3.5).
(3)如图2所示:作△ABC的外接圆Q.过圆心Q作QD⊥AB交圆Q与点P,作点P关于x轴的对称点P′.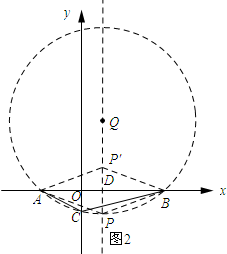
由圆周角定理可知∠ACB=∠APB.
由(2)可知QD=3.5,AD=3.
在Rt△ADQ中,由勾股定理可知:AQ=$\sqrt{{3}^{2}+3.{5}^{2}}$=$\frac{\sqrt{85}}{2}$
∵AQ=QP,
∴点P的坐标为(1,-$\frac{\sqrt{85}-7}{2}$).
∵点P与点P′关于x轴对称,
∴∠AP′B=∠APB=∠ACB,P′(1,$\frac{\sqrt{85}-7}{2}$).
综上所述,点P的坐标为(1,-$\frac{\sqrt{85}-7}{2}$)或P′(1,$\frac{\sqrt{85}-7}{2}$).
点评 本题主要考查的是二次函数的综合应用,解答本题主要应用了外角形的外接圆的性质、圆周角定理、勾股定理、两点间的距离公式、轴对称图形的性质,掌握本题的辅助线的做法是解题的关键.

 新思维假期作业暑假吉林大学出版社系列答案
新思维假期作业暑假吉林大学出版社系列答案 蓝天教育暑假优化学习系列答案
蓝天教育暑假优化学习系列答案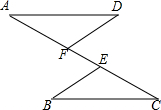 如图,已知AE=CF,AD=BC,DF=BE.
如图,已知AE=CF,AD=BC,DF=BE.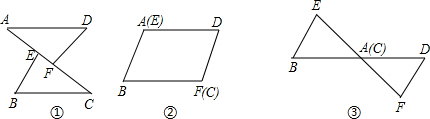
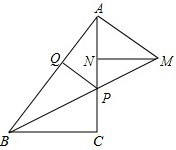 如图,已知:在△ABC中,∠ACB=90°,点P是线段AC上一点,过点A作AB的垂线,交BP的延长线于点M,MN⊥AC于点N,PQ⊥AB于点Q,AQ=MN,NP=2,PC=3.
如图,已知:在△ABC中,∠ACB=90°,点P是线段AC上一点,过点A作AB的垂线,交BP的延长线于点M,MN⊥AC于点N,PQ⊥AB于点Q,AQ=MN,NP=2,PC=3.