题目内容
5.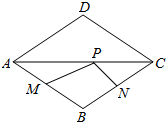 如图,菱形ABCD,∠ABC=120°,点P是AC上一动点,M、N分别是AB、BC的中点,若PM+PN的最小值为2,则对角线AC的长是2$\sqrt{3}$.
如图,菱形ABCD,∠ABC=120°,点P是AC上一动点,M、N分别是AB、BC的中点,若PM+PN的最小值为2,则对角线AC的长是2$\sqrt{3}$.
分析 本题作点M关于AC的对称点M′,根据轴对称性找出点P的位置,从而求出菱形的边长,然后分别求出菱形的两条对角线的长度.
解答 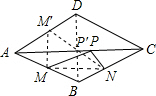 解:作M点关于AC的对称点M′,连接M′N,则与AC的交点P′即是P点的位置.
解:作M点关于AC的对称点M′,连接M′N,则与AC的交点P′即是P点的位置.
∵点M、N分别是边AB、BC的中点,
∴MN是△ABC的中位线,当PM+PN最小时P在AC的中点,
此时,AB=PM+PN=2,
∵∠ABC=120°,
∴∠ABD=60°,
∴△ABD是等边三角形,
连接BD,则BD=AB=2,
AC=2MN=2$\sqrt{{2}^{2}-{1}^{2}}$=2$\sqrt{3}$,
故答案是:2$\sqrt{3}$.
点评 本题考查轴菱形的性质、对称--最短路线问题及菱形的性质.正确确定P点的位置是解题的关键.

练习册系列答案
相关题目
 如图,在?ABCD中,BE平分∠ABC,BC=5,DE=2,求?ABCD的周长.
如图,在?ABCD中,BE平分∠ABC,BC=5,DE=2,求?ABCD的周长.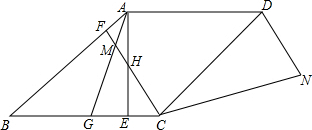 如图,菱形ABCD中,G是BC中点,连接AG,作CF⊥AB于F交AG于M,AE⊥BC交CF于H,现过D作DN平行等于MC;连接CN.
如图,菱形ABCD中,G是BC中点,连接AG,作CF⊥AB于F交AG于M,AE⊥BC交CF于H,现过D作DN平行等于MC;连接CN.