题目内容
15.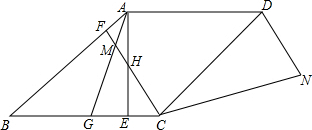 如图,菱形ABCD中,G是BC中点,连接AG,作CF⊥AB于F交AG于M,AE⊥BC交CF于H,现过D作DN平行等于MC;连接CN.
如图,菱形ABCD中,G是BC中点,连接AG,作CF⊥AB于F交AG于M,AE⊥BC交CF于H,现过D作DN平行等于MC;连接CN.(1)若CH=9,求AH的长;
(2)求证:CN=MG+AG.
分析 (1)如图1中,连接AC,只要证明∠BCA=∠BAC,∠BAE=∠BCF即可得到∠HAC=∠HCA,由此即可解决问题.
(2)延长AG到K,使得GK=GM,连接BK,CK,想办法证明△ABK≌△CDN即可解决问题.
解答 (1)解:如图1中,连接AC.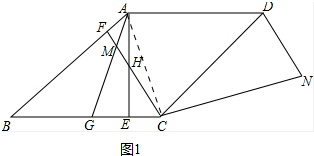
∵四边形ABCD是菱形,
∴AB=BC=CD=DA,
∴∠BCA=∠BAC,
∵AE⊥BC,CF⊥AB,
∴∠AEC=∠CFA=90°,
∴∠B+∠BCF=90°,∠B+∠BAE=90°,
∴∠BAE=∠BCF,
∴∠HAC=∠HCA,
∴AH=HC=9.
(2)证明:如图2中,延长AG到K,使得GK=GM,连接BK,CK,BM,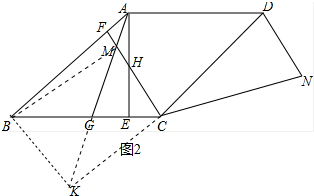 ∵BG=GC,GM=GK,
∵BG=GC,GM=GK,
∴四边形FBKC是平行四边形,
∴CM=BK=DN,BK∥CF,
∵DN∥CM,
∴∠CDN=∠FCD=∠CFB=90°,
∴∠ABK+∠BFC=180°,
∴∠ABK=∠CDN=90°,
在△ABK和△CDN中,
$\left\{\begin{array}{l}{AB=CD}\\{∠ABK=∠CDN}\\{BK=DN}\end{array}\right.$,
∴△ABK≌△CDN,
∴CN=AK=AG+GK=AG+GM.
∴CN=AG+GM.
点评 本题考查菱形的性质、全等三角形的判定和性质、平行四边形的判定和性质、等腰三角形的判定和性质等知识,解题的关键是添加辅助线构造特殊四边形,属于中考常考题型.

练习册系列答案
 赢在课堂名师课时计划系列答案
赢在课堂名师课时计划系列答案 天天向上课时同步训练系列答案
天天向上课时同步训练系列答案 阳光课堂同步练习系列答案
阳光课堂同步练习系列答案
相关题目
7.今年9月,杭州将举办二十国集团领导人峰会,一支有着76万人的平安志愿寻访队伍,参与社会治理,成为一道亮丽的风景,其中76万人用科学记数法表示为( )人.
| A. | 7.6×106 | B. | 76×104 | C. | 7.6×105 | D. | 0.76×106 |
4.羊年除夕当日微信红包收发总量达80.8亿个.其中80.8亿用科学记数法可表示为( )
| A. | 8.08×108 | B. | 0.808×109 | C. | 8.08×109 | D. | 0.808×1010 |
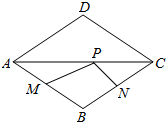 如图,菱形ABCD,∠ABC=120°,点P是AC上一动点,M、N分别是AB、BC的中点,若PM+PN的最小值为2,则对角线AC的长是2$\sqrt{3}$.
如图,菱形ABCD,∠ABC=120°,点P是AC上一动点,M、N分别是AB、BC的中点,若PM+PN的最小值为2,则对角线AC的长是2$\sqrt{3}$. 如图,己知矩形ABCD中,点E是BC边上的一动点,过点E作EF⊥BD于点F,EG⊥AC于点G,CH⊥BD于点H.
如图,己知矩形ABCD中,点E是BC边上的一动点,过点E作EF⊥BD于点F,EG⊥AC于点G,CH⊥BD于点H. 如图,LA,LB分别表示A步行与B骑车在同一路上行驶的路程y(千米)与时间x(小时)的关系.根据图象,回答下列问题:
如图,LA,LB分别表示A步行与B骑车在同一路上行驶的路程y(千米)与时间x(小时)的关系.根据图象,回答下列问题: 如图,一所学校的平面示意图中,如果图书馆的位置记作(3,2),实验楼的位置记作(1,-1),则校门的位置记作(-2,0).
如图,一所学校的平面示意图中,如果图书馆的位置记作(3,2),实验楼的位置记作(1,-1),则校门的位置记作(-2,0).