题目内容

15．已知：如图，在正方形ABCD中，E，F分别AB，AD上的点，又AB=12，EF=10，△AEF的面积等于五边形EBCDF面积的$\frac{1}{5}$，求AE，AF的长．

分析 设AE=x，AF=y，利用勾股定理，以及面积关系列出方程组即可解决问题．

解答 解：设AE=x，AF=y，
由题意$\left\{\begin{array}{l}{{x}^{2}+{y}^{2}=1{0}^{2}}\\{\frac{1}{2}xy=\frac{1}{6}×1{2}^{2}}\end{array}\right.$，
解得$\left\{\begin{array}{l}{x=6}\\{y=8}\end{array}\right.$或$\left\{\begin{array}{l}{x=8}\\{y=6}\end{array}\right.$，
∴AE=6，AF=8或AE=8，AF=6．

点评 本题考查正方形的性质，勾股定理、二元一次方程组等知识，解题的关键是学会利用参数，用方程组的思想思考问题，属于中考常考题型．

练习册系列答案
相关题目
5．抛物线y=ax2+bx+c经过（0，5）、（2，2）、（-8，-3）三点，求它的开口方向，对称轴和顶点坐标．
6．周长是22cm的等腰三角形，其中一边长为6cm，其它两边长分别为（　　）
A．6cm，10cmB．8cm，8cm
C．6cm，10cm或8cm，8cmD．无法确定
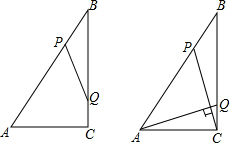3．如图，Rt△ABC中，∠ACB=90°，AC=6cm，BC=8cm，动点P从点B出发，在BA边上以每秒5cm的速度向点A匀速运动，同时动点Q从点C出发，在CB边上以每秒4cm的速度向点B匀速运动，运动时间为t秒（0＜t＜2），连接PQ．
（1）若△BPQ与△ABC相似，求t的值；
（2）试探究t为何值时，△BPQ是等腰三角形；
（3）试探究t为何值时，CP=CQ；
（4）连接AQ，CP，若AQ⊥CP，求t的值．
10．（1）3$\sqrt{20}$-$\sqrt{45}$-$\sqrt{\frac{1}{5}}$
（2）$\sqrt{16}$+$\root{3}{-27}$+3$\sqrt{3}$-$\sqrt{（-3）^{2}}$
（3）（$\sqrt{2}$+$\sqrt{3}$）（$\sqrt{2}$-$\sqrt{3}$）
20．计算题
（1）-14-（-3）2-12×|-$\frac{3}{4}}$|
（2）（-3）2-（1-$\frac{2}{5}$）÷（${-\frac{3}{4}}$）×[4-（-42）]．
7．若关于x的一元二次方程x2-2x-n=0没有实数根，则一次函数y=（n+1）x-n的图象不经过第三象限．
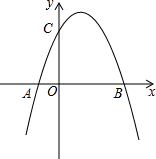4．如图，将抛物线y=-x2+1平移，平移后的抛物线与x轴交于点A（-1，0）和点B（3，0），并与x轴交于点C．
（1）求平移后的抛物线的表达式；
（2）点P是抛物线在第一象限上的一动点，当∠ACB=∠ABP时，求点P的坐标；
（3）在（2）问的条件下，点E是PB的中点，过点P作x轴的平行线交y轴于点F，点M是直线PF上的一个动点，且点M与点P不重合，当∠PME=$\frac{1}{3}$∠MEB是，求点M的坐标．
5．“3.15”植树节活动后，对栽下的甲、乙、丙、丁四个品种的树苗进行成活率观测，以下是根据观测数据制成的统计图表的一部分：
表1 栽下的各品种树苗棵数统计表
植树品种甲种乙种丙种丁种
植树棵数150125125
请你根据以上信息解答下列问题：
（1）将上表补充完整；
（2）图1中，甲30%%、乙20%%，并将图2补充完整；
（3）若经观测计算得出丙种树苗的成活率为89.6%，求这次植树活动的树苗成活率．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网