题目内容
15.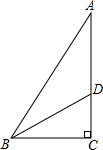 如图,在Rt△ABC中,∠ACB=90°,∠ABC的平分线交AC于点D,BC=12,DB=13,点D到AB的距离是( )
如图,在Rt△ABC中,∠ACB=90°,∠ABC的平分线交AC于点D,BC=12,DB=13,点D到AB的距离是( )| A. | 5 | B. | 6 | C. | 4 | D. | 3 |
分析 作DE⊥AB于E,根据勾股定理求出CD,根据角平分线的性质解答即可.
解答 解:作DE⊥AB于E,
∵∠ACB=90°,BC=12,DB=13,
∴CD=$\sqrt{B{D}^{2}-B{C}^{2}}$=5,
∵BD是∠ABC的平分线,∠ACB=90°,DE⊥AB,
∴DE=CD=5,
故选:A.
点评 本题考查的是角平分线的性质,掌握角的平分线上的点到角的两边的距离相等是解题的关键.

练习册系列答案
相关题目
5.下列事件发生的概率为0的是( )
| A. | 射击运动员只射击1次,就命中10环 | |
| B. | 任取一个有理数x,都有|x|≥0 | |
| C. | 画一个三角形,使其三个内角的和为199° | |
| D. | 抛掷一枚质地均匀且六个面分别刻有1到6的点数的正方体骰子,朝上一面的点数为1 |
3. a、b在数轴上的位置如图所示,则下列式子正确的是( )
a、b在数轴上的位置如图所示,则下列式子正确的是( )
 a、b在数轴上的位置如图所示,则下列式子正确的是( )
a、b在数轴上的位置如图所示,则下列式子正确的是( )| A. | a+b>0 | B. | a+b>a-b | C. | ab<0 | D. | |a|>|b| |
10.一元二次方程x2=2x的根是( )
| A. | x1=0,x2=2 | B. | x=0 | C. | x=2 | D. | x1=0,x2=-2 |
7. 如图,在数轴上点M表示的数可能是( )
如图,在数轴上点M表示的数可能是( )
 如图,在数轴上点M表示的数可能是( )
如图,在数轴上点M表示的数可能是( )| A. | 1.5 | B. | -1.5 | C. | -2.5 | D. | 2.5 |
4.已知五边形ANCDE∽五边形A1B1C1D1E1,五边形ABCDE的最短边为2,最长边为6,五边形A1B1C1D1E1,的最长边是12,则五边形A1B1C1D1E1的最短边是( )
| A. | 4 | B. | 5 | C. | 6 | D. | 8 |
5.关于x的一元二次方程(m+2)x2+3x+m2=4的一根是0,则m的值是( )
| A. | 2 | B. | -2 | C. | 2或-2 | D. | 0 |
 如图,BD是△ABC边AC的中线,点E在BC上,BE=$\frac{1}{2}$EC,△AED的面积是3,则△BED的面积是1.5.
如图,BD是△ABC边AC的中线,点E在BC上,BE=$\frac{1}{2}$EC,△AED的面积是3,则△BED的面积是1.5.