题目内容
20. 如图,BD是△ABC边AC的中线,点E在BC上,BE=$\frac{1}{2}$EC,△AED的面积是3,则△BED的面积是1.5.
如图,BD是△ABC边AC的中线,点E在BC上,BE=$\frac{1}{2}$EC,△AED的面积是3,则△BED的面积是1.5.
分析 利用三角形面积公式,等高的三角形的面积比等于底边的比,则S△AEC=$\frac{2}{3}$S△ABC=6,S△EDC=S△AED=3,S△AEC=2S△AED=6,然后利用S△BED=S△BDC-S△EDC即可得到答案.
解答 解:∵BD是△ABC边AC的中线,△AED的面积是3,
∴S△EDC=S△AED=3,S△AEC=2S△AED=6,
∵BE=$\frac{1}{2}$EC,
∴S△AEC=$\frac{2}{3}$S△ABC=6,
∴S△ABC=9,
∴S△BDC=S△ABD=$\frac{1}{2}$S△ABC=4.5,
∵S△BDC=S${\;}_{△BDE+{S}_{△EDC}}$,S△ABC=S△ABE+S△AEC,
∴S△BED=S△BDC-S△EDC=4.5-3=1.5.
故答案为1.5.
点评 本题考查了三角形面积:三角形的面积等于底边长与高线乘积的一半,即S△=$\frac{1}{2}$×底×高;三角形的中线将三角形分成面积相等的两部分.

练习册系列答案
 优生乐园系列答案
优生乐园系列答案
相关题目
10.甲、乙、丙、丁四名选手参加200米决赛,赛场共设1,2,3,4四条跑道,选手以随机抽签的方式决定各自的跑道,若甲首先抽签,则甲抽到第1道的概率是( )
| A. | 0 | B. | $\frac{1}{4}$ | C. | $\frac{1}{2}$ | D. | 1 |
11.若a2+2a=1,则3a2+6a-2的值是( )
| A. | -1 | B. | 1 | C. | 4 | D. | 2 |
5. 某种股票在7个月内销售增长率的变化情况如图所示,从图上看,下列结论不正确的是( )
某种股票在7个月内销售增长率的变化情况如图所示,从图上看,下列结论不正确的是( )
 某种股票在7个月内销售增长率的变化情况如图所示,从图上看,下列结论不正确的是( )
某种股票在7个月内销售增长率的变化情况如图所示,从图上看,下列结论不正确的是( )| A. | 2~6月股票的销售量增长率逐渐变小 | |
| B. | 7月份股票的销售量增长率开始回升 | |
| C. | 这7个月中,每月的股票销量不断上涨 | |
| D. | 这7个月中,股票销售量有上涨有下跌 |
12.下列各数中描述无理数的是( )
| A. | -3.14 | B. | $\sqrt{31}$ | C. | $\root{3}{-8}$ | D. | $\sqrt{9}$ |
9.某旅游景点的游客人数逐年增加,据有关部门统计,2014年约为21万人次,若2016年约为27万人次,设游客人数年平均增长率为x,则下列方程中正确的是( )
| A. | 20(1+2x)=27 | B. | 27(1+x)2=21 | ||
| C. | 21(1+x)2=27 | D. | 21+21(1+x)+20(1+x)2=27 |
10.某班共有a名学生,其中男生人数占40%,那么女生人数为( )
| A. | 40%a | B. | (1-40%)a | C. | $\frac{a}{40%}$ | D. | $\frac{a}{1-40%}$ |
 在正方体的表面上画有图(1)中所示的线,图(2)是其展开图的示意图,但只在A面上画有线,那么将图1中剩余两个面中的线画入图(2)中,画法正确的是( )
在正方体的表面上画有图(1)中所示的线,图(2)是其展开图的示意图,但只在A面上画有线,那么将图1中剩余两个面中的线画入图(2)中,画法正确的是( )



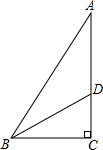 如图,在Rt△ABC中,∠ACB=90°,∠ABC的平分线交AC于点D,BC=12,DB=13,点D到AB的距离是( )
如图,在Rt△ABC中,∠ACB=90°,∠ABC的平分线交AC于点D,BC=12,DB=13,点D到AB的距离是( )