题目内容
8．
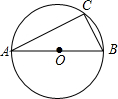如图，AB是⊙O的直径，点C是⊙O上一点，若BC=1，AC=2，则OB的长度是$\frac{\sqrt{5}}{2}$．
分析 由AB是⊙O的直径，得到∠ACB=90°，利用勾股定理可求出AB的长度，继而求得该圆的半径．
解答 解：如图，∵AB是⊙O的直径，
∴∠ACB=90°，
又∵BC=1，AC=2，
∴AB=$\sqrt{A{C}^{2}+B{C}^{2}}$=$\sqrt{{2}^{2}+{1}^{2}}$=$\sqrt{5}$，
则OB=$\frac{1}{2}$AB=$\frac{\sqrt{5}}{2}$．
故答案是：$\frac{\sqrt{5}}{2}$．
点评 本题考查了圆周角定理和勾股定理．根据圆周角定理求得∠ACB=90°是解题的关键．
练习册系列答案
名校课堂系列答案
相关题目
如图，从一个直径为4的圆形铁片中剪下一个圆心角为90°的扇形ABC．求这个扇形的面积．
17．
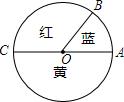一个转盘的颜色如图所示，其中∠AOB=60°，∠BOC=120°，则转动转盘时，指针落在红色区域的概率是（ ）
一个转盘的颜色如图所示，其中∠AOB=60°，∠BOC=120°，则转动转盘时，指针落在红色区域的概率是（ ）| A． | $\frac{1}{6}$ | B． | $\frac{1}{3}$ | C． | $\frac{1}{2}$ | D． | $\frac{2}{3}$ |
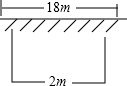如图，有一面积是150平方米的长方形鸡场，鸡场的一边靠墙（墙长18米），墙对面有一个2米宽的门，另三边用竹篱笆围成，篱笆总长33米，