题目内容
13.在Rt△ABC中,∠ACB=90°,tan∠CAB=$\frac{3}{4}$,AB=10,点P在直线AB上,PB=6,则PC=$\frac{12\sqrt{5}}{5}$.分析 先求出AC,BC,进而求出AP,PD,AD,即可求出CD,最后用勾股定理即可得出结论.
解答 解:如图,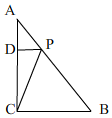 过点P作PD⊥AC,
过点P作PD⊥AC,
在Rt△ABC中,tan∠CAB=$\frac{3}{4}$,AB=10,
∴BC=6,AC=8,
∵PB=6,
∴AP=4,
在Rt△PAD中,tan∠CAB=$\frac{3}{4}$,AP=4,
∴AD=$\frac{16}{5}$,PD=$\frac{12}{5}$,
∴CD=AC-AD=$\frac{24}{5}$,
根据勾股定理得,PC=$\sqrt{P{D}^{2}+C{D}^{2}}$=$\frac{12\sqrt{5}}{5}$
故答案为$\frac{12\sqrt{5}}{5}$,
点评 此题是解直角三角形,主要考查了勾股定理,锐角三角函数,解本题的关键是构造出直角三角形ADP.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
1.点 A(3,2)在双曲线y=$\frac{k}{x}$上,则k的值为( )
| A. | 1 | B. | 2 | C. | 3 | D. | 6 |
8.已知反比例函数y=(a-2)${x^{{a^2}-4a+2}}$的图象位于第二、四象限,则a的值为( )
| A. | 1 | B. | 3 | C. | -1 | D. | -3 |
18.绝对值大于π而不大于6的所有正整数之和为( )
| A. | 0 | B. | 9 | C. | 10 | D. | 15 |
5.已知⊙O的直径为6cm,点A不在⊙O内,则OA的长( )
| A. | 大于3cm | B. | 不小于3cm | C. | 大于6cm | D. | 不小于6cm |