题目内容
2.某地2014年为做好“精准扶贫”,投入资金1280万元用于异地安置,并规划投入资金逐年增加,2016年投入资金2880万元.(1)从2014年到2016年,该地投入异地安置资金的年平均增长率为多少?
(2)在2016年异地安置的具体实施中,该地计划投入资金不低于500万元用于优先搬迁租房奖励,规定前1000户(含第1000户)每户每天奖励8元,1000户以后每户每天奖励5元,按租房400天计算,试求今年该地至少有多少户享受到优先搬迁租房奖励?
分析 (1)设年平均增长率为x,根据:2014年投入资金给×(1+增长率)2=2016年投入资金,列出方程组求解可得;
(2)设今年该地有a户享受到优先搬迁租房奖励,根据:前1000户获得的奖励总数+1000户以后获得的奖励总和≥500万,列不等式求解可得.
解答 解:(1)设该地投入异地安置资金的年平均增长率为x,根据题意得:
1280(1+x)2=2880
解得:x1=$\frac{1}{2}$,x2=-$\frac{5}{2}$(不合题意,应舍去),
答:从2014年到2016年,该地投入异地安置资金的年平均增长率为50%;
(2)设今年该地有a户享受到优先搬迁租房奖励,根据题意得:
1000×8×400+(a-1000)×5×400≥5000000
解得:a≥1900
答:今年该地至少有1900户享受到优先搬迁租房奖励.
点评 本题主要考查一元二次方程与一元一次不等式的应用,由题意准确抓住相等关系并据此列出方程或不等式是解题的关键.

练习册系列答案
相关题目
10.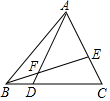 D、E分别为△ABC中BC、AC边上的点,且BD:DC=1:3,AE:EC=2:1,则AF:FD=( )
D、E分别为△ABC中BC、AC边上的点,且BD:DC=1:3,AE:EC=2:1,则AF:FD=( )
 D、E分别为△ABC中BC、AC边上的点,且BD:DC=1:3,AE:EC=2:1,则AF:FD=( )
D、E分别为△ABC中BC、AC边上的点,且BD:DC=1:3,AE:EC=2:1,则AF:FD=( )| A. | 3:1 | B. | 5:1 | C. | 8:1 | D. | 9:1 |
17.方程x2-x=2的根的判别式的值是( )
| A. | -7 | B. | 9 | C. | ±3 | D. | -9 |
7.如果一个数的绝对值比它本身大,那么这个数为( )
| A. | 正数 | B. | 负数 | ||
| C. | 整数 | D. | 不等于零的有理数 |
14.下列命题中,真命题的个数是( )
①经过三点一定可以作圆;
②任意一个圆一定有一个内接三角形,并且只有一个内接三角形.
③任意一个三角形一定有一个外接圆,并且只有一个外接圆;
④三角形的内心到三角形的三个顶点距离相等.
①经过三点一定可以作圆;
②任意一个圆一定有一个内接三角形,并且只有一个内接三角形.
③任意一个三角形一定有一个外接圆,并且只有一个外接圆;
④三角形的内心到三角形的三个顶点距离相等.
| A. | 4个 | B. | 3个 | C. | 2个 | D. | 1个 |
11.若一个数的绝对值的相反数是-$\frac{1}{7}$,则这个数是( )
| A. | -$\frac{1}{7}$ | B. | +$\frac{1}{7}$ | C. | ±$\frac{1}{7}$ | D. | ±7 |
12. 有理数a,b在数轴上对应的位置如图,则( )
有理数a,b在数轴上对应的位置如图,则( )
 有理数a,b在数轴上对应的位置如图,则( )
有理数a,b在数轴上对应的位置如图,则( )| A. | a+b<0 | B. | a+b>0 | C. | a-b=0 | D. | a-b>0 |