题目内容
17．
如图，△ABC的∠B的外角的平分线BD与∠C的外角的平分线CE相交于点P，若点P到AC的距离为3，则点P到AB的距离为（ ）| A． | 1 | B． | 2 | C． | 3 | D． | 4 |
分析 过P作PQ⊥AC于Q，PW⊥BC于W，PR⊥AB于R，根据角平分线性质得出PQ=PR，即可得出答案．
解答 解：
过P作PQ⊥AC于Q，PW⊥BC于W，PR⊥AB于R，
∵△ABC的∠B的外角的平分线BD与∠C的外角的平分线CE相交于点P，
∴PQ=PW，PW=PR，
∴PR=PQ，
∵点P到AC的距离为3，
∴PQ=PR=3，
则点P到AB的距离为3，
故选C．
点评 本题考查了角平分线性质的应用，能灵活运用性质进行推理是解此题的关键，注意：角平分线上的点到角两边的距离相等．
练习册系列答案
相关题目
7．下列命题是假命题的是（ ）
| A． | 有一个角为60°的等腰三角形是等边三角形 | |
| B． | 等角的补角相等 | |
| C． | 锐角三角形每个角都小于90° | |
| D． | 内错角相等 |
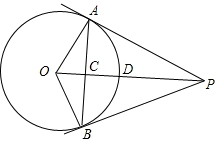如图所示，PA，PB是⊙O的两条切线，A，B为切点，连接PO，交⊙O于点D，交AB于点C．
如图是由正方形ABCD和直角梯形DEFC组成的图形，已知正方形ABCD的面积为100，求阴影部分面积？