Question

4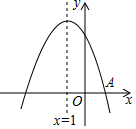．如图，抛物线y=ax²+bx+c与x轴的一个交点是A（1，0），对称轴为直线x=-1，则一元二次方程ax²+bx+c=0的解是x₁=1，x₂=-3．

Answer 1

分析 直接利用抛物线的对称性以及结合对称轴以及抛物线y=ax²+bx+c与x轴的一个交点是A（1，0），得出另一个与x轴的交点，进而得出答案．

解答 解：∵抛物线y=ax²+bx+c与x轴的一个交点是A（1，0），对称轴为直线x=-1，
∴抛物线y=ax²+bx+c与x轴的另一个交点是（-3，0），
∴一元二次方程ax²+bx+c=0的解是：x₁=1，x₂=-3．
故答案为：x₁=1，x₂=-3．

点评 此题主要考查了抛物线与x轴的交点，正确得出抛物线与x轴的交点坐标是解题关键．