题目内容
7.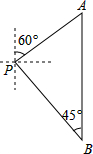 如图,小明从P点出发,沿北偏东60°方向行驶到达A处,接着向正南方向行驶100($\sqrt{3}$+1)米到达B处.在B处观测到出发时所在的P处在北偏西45°方向上,P,A两处相距多少米?
如图,小明从P点出发,沿北偏东60°方向行驶到达A处,接着向正南方向行驶100($\sqrt{3}$+1)米到达B处.在B处观测到出发时所在的P处在北偏西45°方向上,P,A两处相距多少米?
分析 作辅助线PC⊥AB交AB于点C,设BC长度为x,则AC=AB-BC=100($\sqrt{3}$+1)-x,在△PBC根据∠B=45°,可得BC=PC=x,然后在△PAC中根据三角函数求出PA的长度.
解答 解:作辅助线PC⊥AB交AB于点C,
设BC长度为x,则AC=AB-BC=100($\sqrt{3}$+1)-x,
在△PBC中,
∵∠B=45°,
∴BC=PC=x,
在△PAC中,
∵∠APC=90°-60°=30°,
∴tan30°=$\frac{AC}{PC}$=$\frac{100(\sqrt{3}+1)-x}{x}$=$\frac{\sqrt{3}}{3}$,
化简得:300($\sqrt{3}$+1)-3x=$\sqrt{3}$x,
解得:x=$\frac{200\sqrt{3}}{3}$,
∵cos30°=$\frac{PC}{PA}$=$\frac{\sqrt{3}}{2}$,
∴PA=$\frac{2\sqrt{3}}{3}$PC=$\frac{2\sqrt{3}}{3}$×$\frac{200\sqrt{3}}{3}$=$\frac{400}{3}$.
答:P,A两处相距$\frac{400}{3}$米.
点评 本题主要考查了方向角的含义和解直角三角形的应用,解答本题的关键在于读懂题意,根据所给方向角做出合适的辅助线,构造直角三角形,利用三角函数的知识来进行求解.

练习册系列答案
 53天天练系列答案
53天天练系列答案
相关题目
17.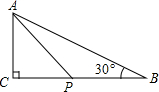 如图,△ABC中,∠C=90°,AC=2.5,∠B=30°,点P是BC边上的动点,则AP长不可能是( )
如图,△ABC中,∠C=90°,AC=2.5,∠B=30°,点P是BC边上的动点,则AP长不可能是( )
 如图,△ABC中,∠C=90°,AC=2.5,∠B=30°,点P是BC边上的动点,则AP长不可能是( )
如图,△ABC中,∠C=90°,AC=2.5,∠B=30°,点P是BC边上的动点,则AP长不可能是( )| A. | 3 | B. | 3.5 | C. | 4.8 | D. | 5.2 |
15. 如图,直角三角板的直角顶点落在直尺边上,若∠1=56°,则∠2的度数为( )
如图,直角三角板的直角顶点落在直尺边上,若∠1=56°,则∠2的度数为( )
 如图,直角三角板的直角顶点落在直尺边上,若∠1=56°,则∠2的度数为( )
如图,直角三角板的直角顶点落在直尺边上,若∠1=56°,则∠2的度数为( )| A. | 34° | B. | 44° | C. | 56° | D. | 28° |
12.若二次函数y=x2-6x+9的图象经过A(-1,y1),B(1,y2),C(3+$\sqrt{3}$,y3)三点.则关于y1,y2,y3大小关系正确的是( )
| A. | y1>y2>y3 | B. | y1>y3>y2 | C. | y2>y1>y3 | D. | y3>y1>y2 |
19.下列四组数分别是三条线段的长度,能构成三角形的是( )
| A. | 1,1,2 | B. | 1,3,4 | C. | 2,3,6 | D. | 4,5,8 |
 如图,二次函数y=ax2+bx+c(a≠0)的图象与x轴交于A,B两点,与y轴交于点C,且OA=OC,则下列结论:①abc<0;②$\frac{{b}^{2}-4ac}{4a}>0$;③ac-b+1=0;④OA•OB=-$\frac{c}{a}$.其中正确结论的序号是①③④.
如图,二次函数y=ax2+bx+c(a≠0)的图象与x轴交于A,B两点,与y轴交于点C,且OA=OC,则下列结论:①abc<0;②$\frac{{b}^{2}-4ac}{4a}>0$;③ac-b+1=0;④OA•OB=-$\frac{c}{a}$.其中正确结论的序号是①③④.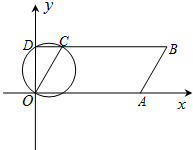 如图,在平面直角坐标系中,以OC为直径的圆交y轴于点D,∠DOC=30°,OC=2.延长DC至点B,使得CB=4DC,过B点作BA∥OC交x轴于A点.
如图,在平面直角坐标系中,以OC为直径的圆交y轴于点D,∠DOC=30°,OC=2.延长DC至点B,使得CB=4DC,过B点作BA∥OC交x轴于A点.