Question

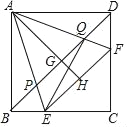
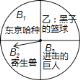
【题目】已知：正方形ABCD中，AB=4，E为CD边中点，F为AD边中点，AE交BD于G，交BF于H，连接DH．

（1）求证：BG=2DG；

（2）求AH：HG：GE的值；

（3）求的值．

Answer 1

【答案】（1）详见解析；（2）AH：HG：GE =6：4：5；（3）.

【解析】

（1）利用平行线分线段成比例定理即可解决问题；
（2）分别求出AH、GH、GE即可解决问题；
（3）作DM⊥AE于M．分别求出DH、BH即可；

（1）证明：∵四边形ABCD是正方形，

∵AB∥CD，AB=CD，

∵E为CD边中点，

∴ ,

∴，

∴BG=2DG．

（2）解：∵AB∥CD，AB=CD，

∵E为CD边中点，

∴

∴，

∴ ,

在Rt△ADE中，∵AD=4，DE=2，

∴AE=，

∴EG=，

同理可得BF=,

∵AB=AD，∠BAF=∠ADE，AF=DE，

∴△BAF≌△ADE，

∴∠ABF=∠DAE，

∵∠DAE+∠BAH=90°，

∴∠ABF+∠BAH=90°，

∴∠AHB=90°，

∴AE⊥BF，

∴ ,

∴AH=，

∴HG=2，

∴AH：HG：GE= =6：4：5．

（3）作DM⊥AE于M．

由（2）可知：DM=AH=，

在Rt△DME中，

∴EM==，

∴HM=AE-AH-EM=2 - -=，

在Rt△DHM中，

∴DH= =，

在Rt△AHB中，

∵BH==，

∴=．