题目内容
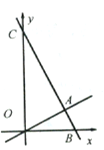
【题目】如图，在平面直角坐标系中，抛物线y=﹣x2+ 
与y轴相交于点A，点B与点O关于点A对称．
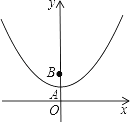
（1）填空：点B的坐标为________；
（2）过点B的直线y=kx+b（其中k＜0）与x轴相交于点C，过点C作直线l平行于y轴，P是直线l上一点，且PB=PC，求线段PB的长（用含k的式子表示），并判断点P是否在抛物线上，说明理由．
【答案】（1）（0， 
）；（2）PB=
+
，点P在抛物线上
【解析】
（1）由抛物线解析式可求得A点坐标，再利用对称可求得B点坐标；
（2）可先用k表示出C点坐标，过B作BD⊥l于点D，条件可知P点在x轴上方，设P点纵坐标为y，可表示出PD、PB的长．在Rt△PBD中，利用勾股定理可求得y，则可求出PB的长，此时可得出P点坐标，代入抛物线解析式可判断P点在抛物线上．
（1）∵y=﹣x2+的顶点A的坐标为（0，），∴原点O关于点A的对称点B的坐标为（0，）．
故答案为：（0，）；
（2）∵B点坐标为（0，），∴直线解析式为y=kx+，解得：x=﹣
，∴OC=﹣．
∵PB=PC，∴点P只能在x轴上方，如图，过点B作BD⊥l于点D，设PB=PC=m，则BD=OC=﹣，CD=OB=，∴PD=PC﹣CD=m﹣．
在Rt△PBD中，由勾股定理可得：PB2=PD2+BD2，即m2=（m﹣）2+（﹣）2，解得：m=+，∴PB=+，∴点P坐标为（﹣
+）．
当x=﹣时，代入抛物线解析式可得：y=+，∴点P在抛物线上．
练习册系列答案
相关题目
