题目内容
7. 如图,点D、F在线段AB上,点E、G分别在线段BC和AC上,CD∥EF,∠1=∠2.
如图,点D、F在线段AB上,点E、G分别在线段BC和AC上,CD∥EF,∠1=∠2.(1)判断DG与BC的位置关系,并说明理由;
(2)如果DG是角∠ADC的平分线,∠3=85°,且∠DCE:∠DCG=9:10,说明AB和CD又怎样的位置关系.
分析 (1)根据平行线的性质得出∠2=∠DCB,求出∠1=∠DCB,根据平行线的判定得出即可;
(2)根据平行线的性质求出∠BCG=180°-∠3=95°,求出∠DCG=45°,根据平行的性质求出∠CDG=45°,根据角平分线定义求出∠ADC即可得出答案.
解答 解:(1)∵DG∥BC,理由如下:
∵CD∥EF,
∴∠2=∠DCB,
又∵∠1=∠2,
∴∠1=∠DCB,
∴DG∥BC;
(2)CD⊥AB,理由如下:
由(1)知DG∥BC,
∵∠3=85°,
∴∠BCG=180°-∠3=95°,
∵∠DCE:∠DCG=9:10,
∴∠DCG=95°×$\frac{9}{10}$=45°,
∵DG∥BC,
∴∠CDG=45°,
∵DG是∠ADC的平分线,
∴∠ADC=2∠CDG=90°,
∴CD⊥AB.
点评 本题考查了平行线的性质和判定,角平分线定义,垂直定义等知识点,能熟练地运用定理进行推理是解此题的关键,注意:平行线的性质有:①两直线平行,同位角相等,②两直线平行,内错角相等,③两直线平行,同旁内角互补,反之亦然.

练习册系列答案
相关题目
8.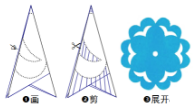 剪纸是中国古老的汉族传统民间艺术之一.下面是制作剪纸的简单流程,展开后的剪纸图案从对称性来判断( )
剪纸是中国古老的汉族传统民间艺术之一.下面是制作剪纸的简单流程,展开后的剪纸图案从对称性来判断( )
 剪纸是中国古老的汉族传统民间艺术之一.下面是制作剪纸的简单流程,展开后的剪纸图案从对称性来判断( )
剪纸是中国古老的汉族传统民间艺术之一.下面是制作剪纸的简单流程,展开后的剪纸图案从对称性来判断( )| A. | 是轴对称图形但不是中心对称图形 | |
| B. | 是中心对称图形但不是轴对称图形 | |
| C. | 既是轴对称图形也是中心对称图形 | |
| D. | 既不是轴对称图形也不是中心对称图形 |
18.下列四边形中不一定为菱形的是( )
| A. | 对角线相等的平行四边形 | |
| B. | 每条对角线平分一组对角的四边形 | |
| C. | 对角线互相垂直的平行四边形 | |
| D. | 用两个全等的等边三角形拼成的四边形 |
 如图,直线AB与CD相交于点O,且∠1+∠2=60°,∠AOD的度数为150°.
如图,直线AB与CD相交于点O,且∠1+∠2=60°,∠AOD的度数为150°. 如图,宽为50的大长方形是由10个形状相同、大小相等的小长方形拼成,其中一个小长方形的面积为400.
如图,宽为50的大长方形是由10个形状相同、大小相等的小长方形拼成,其中一个小长方形的面积为400.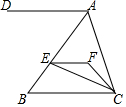 如图,EF∥AD,AD∥BC,∠DAC=120°.
如图,EF∥AD,AD∥BC,∠DAC=120°. 如图,∠1+∠2=180°,∠B=∠3.
如图,∠1+∠2=180°,∠B=∠3.