题目内容
某包装生产企业承接了一批礼品盒制作业务,该企业用规格是170cm×40cm的标准板材作为原材料,每张标准板材按照裁法一或裁法二裁下A型与B型两种板材,如图1(单位:cm).
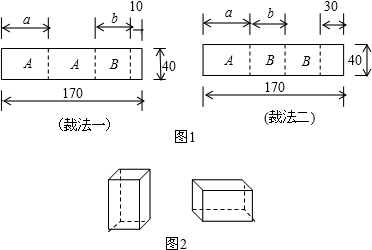
(1)试求出图1中a与b的值;
(2)若将30张标准板材按裁法一裁剪,4张标准板材按裁法二裁剪,裁剪后将得到的A型与B型板材做侧面或底面,做成如图2的竖式与横式两种无盖礼品盒若干.
①按上述方法裁剪后一共可产生A型板材 张,B型板材 张;
②求可以做成的竖式和横式两种无盖礼品盒总数的最大值.

(1)试求出图1中a与b的值;
(2)若将30张标准板材按裁法一裁剪,4张标准板材按裁法二裁剪,裁剪后将得到的A型与B型板材做侧面或底面,做成如图2的竖式与横式两种无盖礼品盒若干.
①按上述方法裁剪后一共可产生A型板材
②求可以做成的竖式和横式两种无盖礼品盒总数的最大值.
考点:二元一次方程组的应用
专题:
分析:(1)根据标准板材的长为170cm,宽为40cm,列方程组,求出a,b的值;
(2)①按照截法1可截出2块A型板材,1块B型板材,按照截法二可截出1块A型纸板,2块B型纸板,求出裁剪后一共可产生A型板材和B型板材;
②设做成的竖式和横式两种无盖礼品盒总数为x个,根据题意可得:5x≤64+38,求出x的取值范围,然后根据礼盒数为正整数,求出x的最大整数解即可.
(2)①按照截法1可截出2块A型板材,1块B型板材,按照截法二可截出1块A型纸板,2块B型纸板,求出裁剪后一共可产生A型板材和B型板材;
②设做成的竖式和横式两种无盖礼品盒总数为x个,根据题意可得:5x≤64+38,求出x的取值范围,然后根据礼盒数为正整数,求出x的最大整数解即可.
解答:解:(1)根据题意,得:
,
解得:
.
故a与b的值分别为60与40;
(2)①两种裁法共产生A型板材为:30×2+4×1=64(张),
B型板材为:30×1+4×2=38(张),
故答案为:64,38;
②设做成的竖式和横式两种无盖礼品盒总数为x个,
依题意得,5x≤64+38,
解得;x≤20.4,
∵x为正整数,
∴x取最大正整数20,
即做成的竖式和横式两种无盖礼品盒总数的最大值是20个.
|
解得:
|
故a与b的值分别为60与40;
(2)①两种裁法共产生A型板材为:30×2+4×1=64(张),
B型板材为:30×1+4×2=38(张),
故答案为:64,38;
②设做成的竖式和横式两种无盖礼品盒总数为x个,
依题意得,5x≤64+38,
解得;x≤20.4,
∵x为正整数,
∴x取最大正整数20,
即做成的竖式和横式两种无盖礼品盒总数的最大值是20个.
点评:本题考查了二元一次方程组的应用,解答本题的关键是读懂题意,设出未知数,找出合适的等量关系,列方程组求解.

练习册系列答案
 长江作业本同步练习册系列答案
长江作业本同步练习册系列答案
相关题目
定义一种新运算“*”,规定:a*b=
a-4b,则12*(-1)=( )
| 1 |
| 3 |
| A、-8 | B、8 | C、-12 | D、11 |
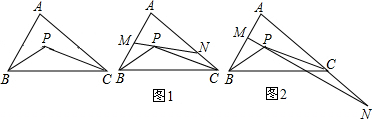

 如图,在边长为1的正方形组成的网格中,△AOB的顶点均在格点上,点A、B的坐标分别是A(3,2),B(1,3),△AOB关于y轴对称的图形为△A1OB1.
如图,在边长为1的正方形组成的网格中,△AOB的顶点均在格点上,点A、B的坐标分别是A(3,2),B(1,3),△AOB关于y轴对称的图形为△A1OB1.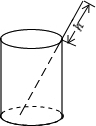 如图,一根长18cm的筷子置于底面半径为5cm.高为12cm圆柱形水杯中,露在水杯外面的长度hcm,则h的取值范围是
如图,一根长18cm的筷子置于底面半径为5cm.高为12cm圆柱形水杯中,露在水杯外面的长度hcm,则h的取值范围是