��Ŀ����
2��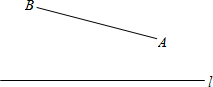 ��һ��ƽ��Ӱ�lͬ����A��B������ׯ��A��B��l�ľ���ֱ�Ϊ3km��2km��AB=xkm��x��1�����ּƻ��ںӰ�l�Ͻ���ˮվP������ˮ�ܵ���������ׯ��ˮ��
��һ��ƽ��Ӱ�lͬ����A��B������ׯ��A��B��l�ľ���ֱ�Ϊ3km��2km��AB=xkm��x��1�����ּƻ��ںӰ�l�Ͻ���ˮվP������ˮ�ܵ���������ׯ��ˮ��������ƣ�
����һ����÷����йܵ�����Ϊy1����y1=PB+BA������PB��l�ڵ�P��
����������÷����йܵ�����Ϊy2����y2=PA+PB�����е�A���ڵ�A����l�Գƣ�A��B��l���ڵ�P��
��x������ȡֵ������з�����Ҫʹ����Ĺܵ����Ƚ϶̣�Ӧ���ѡ�������ַ�����
���� ����һ��PB��l�ڵ�P��y1=PB+BA�����뼴�ɵõ����ۣ�
����������ͼ1������A����l�Գ�A�䣬����A��B��l���ڵ�P����B�� BC��AA����C�����ݹ��ɶ����õ�BC2=x2-1�����A��B=$\sqrt{B{C}^{2}+A��{C}^{2}}$=$\sqrt{{x}^{2}+24}$�����ǵõ�y2=PA+PB=PA��+PB=$\sqrt{{x}^{2}+24}$��
����������۵�y1��y2��y1=y2��y1��y2ʱ�Ϳ��Էֱ����x�ķ�Χ���Ӷ�ȷ��ѡ����
���  �⣺����һ����PB��l�ڵ�P��y1=PB+BA��
�⣺����һ����PB��l�ڵ�P��y1=PB+BA��
��y1=��2+x��km��
����������ͼ1������A����l�Գ�A�䣬����A��B��l���ڵ�P��
��B�� BC��AA����C��
��AC=1��AB=x��A��C=5��
��BC2=x2-1��
��A��B=$\sqrt{B{C}^{2}+A��{C}^{2}}$=$\sqrt{{x}^{2}+24}$��
��y2=PA+PB=PA��+PB=$\sqrt{{x}^{2}+24}$��
��y12-y22=��x+2��2-��$\sqrt{{x}^{2}+24}$��2=4x-20��
��ٵ�4x-20��0����x��5ʱ��y1��y2��
��ѡ��������ܵ��϶̣�
�ڵ�4x-20=0��x=5ʱ��y1=y2��
��ѡ��һ��������ܵ�һ������
�۵�4x-20��0����x��5ʱ��y1��y2��
��ѡ��һ����ܵ��϶̣�
���Ͽ�֪����x��5ʱ��ѡ��������
��x=5ʱ��ѡ����һ������
��1��x��5 ʱ��ѡ����һ��
���� ���⿼������ԳƵ����ʵ����ã����·��������ѧģʽ�����ã����ɶ��������ã����Ĵ�С�ıȽϷ��������ã�

 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�| A�� | ��� | B�� | ֱ�� | C�� | �۽� | D�� | ��ȷ�� |
| ʱ��t/min | 12��t��16 | 16��t��20 | 20��t��24 | 24��t��28 | �ϼ� |
| ���� | 6 | 12 | 14 | 8 | 40 |
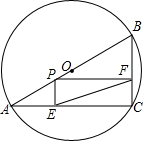 ��ͼ����C����ABΪֱ���ġ�O�ϣ�AC=4��BC=3��PΪֱ��AB��һ���㣬��PE��AC��E��PF��BC��F��
��ͼ����C����ABΪֱ���ġ�O�ϣ�AC=4��BC=3��PΪֱ��AB��һ���㣬��PE��AC��E��PF��BC��F��