题目内容
12.计算|$\sqrt{3}-2$|+2cos30°+$\sqrt{8}$.分析 直接利用绝对值的性质以及特殊角的三角函数值和二次根式的性质化简求出即可.
解答 解:|$\sqrt{3}-2$|+2cos30°+$\sqrt{8}$
=2-$\sqrt{3}$+2×$\frac{\sqrt{3}}{2}$+2$\sqrt{2}$
=2+2$\sqrt{2}$.
点评 此题主要考查了实数运算,正确掌握绝对值的性质是解题关键.

练习册系列答案
相关题目
7.下列方程是关于x的一元二次方程的是( )
| A. | ax2+bx+c=0 | B. | $\frac{1}{{x}^{2}}+\frac{1}{x}$=2 | C. | x2+2x=x2-1 | D. | 3(x+1)2=2(x+1) |
4.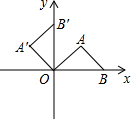 将等腰直角三角形AOB按如图所示放置,然后绕点O逆时针旋转90°至△A′OB′的位置,点B的横坐标为2,则点A′的坐标为( )
将等腰直角三角形AOB按如图所示放置,然后绕点O逆时针旋转90°至△A′OB′的位置,点B的横坐标为2,则点A′的坐标为( )
 将等腰直角三角形AOB按如图所示放置,然后绕点O逆时针旋转90°至△A′OB′的位置,点B的横坐标为2,则点A′的坐标为( )
将等腰直角三角形AOB按如图所示放置,然后绕点O逆时针旋转90°至△A′OB′的位置,点B的横坐标为2,则点A′的坐标为( )| A. | (1,1) | B. | (-1,1) | C. | (1,-1) | D. | $(-\sqrt{2},\sqrt{2})$ |
1.以下列各组数作为三角形的边长,能构成直角三角形的是( )
| A. | 4,5,6 | B. | 6,8,11 | C. | 1,1,$\sqrt{2}$ | D. | 5,12,23 |
2.在图示的汽车标志图案中,能用平移变换(不考虑颜色)来分析其形成过程的图案有( )

| A. | 2个 | B. | 3个 | C. | 4个 | D. | 5个 |
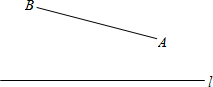 在一个平面河岸l同侧有A、B两个村庄,A、B到l的距离分别为3km和2km,AB=xkm(x>1),现计划在河岸l上建抽水站P,用输水管道向两个村庄供水.
在一个平面河岸l同侧有A、B两个村庄,A、B到l的距离分别为3km和2km,AB=xkm(x>1),现计划在河岸l上建抽水站P,用输水管道向两个村庄供水.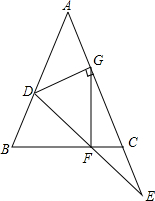 如图,在△ABC中,AB=AC,D是AB上一点,点E在AC的延长线上,且BD=CE,连结DE交BC于F,过点D作DG⊥AE,垂足为G,连结FG.若FG=$\sqrt{2}$,∠E=30°,则GE=$\sqrt{6}$.
如图,在△ABC中,AB=AC,D是AB上一点,点E在AC的延长线上,且BD=CE,连结DE交BC于F,过点D作DG⊥AE,垂足为G,连结FG.若FG=$\sqrt{2}$,∠E=30°,则GE=$\sqrt{6}$.