题目内容
17.平行四边形相邻两内角的平分线相交所成的角是( )| A. | 锐角 | B. | 直角 | C. | 钝角 | D. | 无法确定 |
分析 由平行四边形的性质得出AD∥BC,得出同旁内角互补∠BAD+∠ABC=180°,由角平分线的定义得出∠BAE+∠ABE=$\frac{1}{2}$(∠BAD+∠ABC)=90°,即可得出结果.
解答 解:如图所示:
∵四边形ABCD是平行四边形,
∴AD∥BC,
∴∠BAD+∠ABC=180°,
∵AE、BE分别平分∠BAD、∠ABC,
∴∠BAE=$\frac{1}{2}$∠BAD,∠ABE=$\frac{1}{2}$∠ABC,
∴∠BAE+∠ABE=$\frac{1}{2}$(∠BAD+∠ABC)=$\frac{1}{2}$×180°=90°;
故选:B.
点评 本题考查了平行四边形的性质、角平分线的定义;熟练掌握平行四边形的性质,并能进行推理计算是解决问题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
9. 如图EF∥GF∥IJ∥BC,共有( )对相似的三角形.
如图EF∥GF∥IJ∥BC,共有( )对相似的三角形.
 如图EF∥GF∥IJ∥BC,共有( )对相似的三角形.
如图EF∥GF∥IJ∥BC,共有( )对相似的三角形.| A. | 4对 | B. | 5对 | C. | 6对 | D. | 7对 |
6.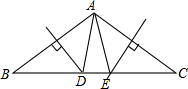 如图,△ABC中,AB、AC的垂直平分线分别交BC于D、E,且∠DAE=20°,则∠BAC=( )
如图,△ABC中,AB、AC的垂直平分线分别交BC于D、E,且∠DAE=20°,则∠BAC=( )
 如图,△ABC中,AB、AC的垂直平分线分别交BC于D、E,且∠DAE=20°,则∠BAC=( )
如图,△ABC中,AB、AC的垂直平分线分别交BC于D、E,且∠DAE=20°,则∠BAC=( )| A. | 100° | B. | 120° | C. | 150° | D. | 160° |
7.下列方程是关于x的一元二次方程的是( )
| A. | ax2+bx+c=0 | B. | $\frac{1}{{x}^{2}}+\frac{1}{x}$=2 | C. | x2+2x=x2-1 | D. | 3(x+1)2=2(x+1) |
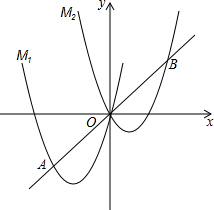 如图,将抛物线M1:y1=ax2+4x向右平移3个单位,再向上平移3个单位,得到抛物线y2,记为M2,直线y=x与M1
如图,将抛物线M1:y1=ax2+4x向右平移3个单位,再向上平移3个单位,得到抛物线y2,记为M2,直线y=x与M1
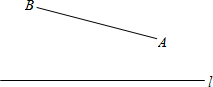 在一个平面河岸l同侧有A、B两个村庄,A、B到l的距离分别为3km和2km,AB=xkm(x>1),现计划在河岸l上建抽水站P,用输水管道向两个村庄供水.
在一个平面河岸l同侧有A、B两个村庄,A、B到l的距离分别为3km和2km,AB=xkm(x>1),现计划在河岸l上建抽水站P,用输水管道向两个村庄供水.