题目内容
 如图,AB是⊙O的弦,半径OA=20cm,∠AOB=120°,求线段AB的长.
如图,AB是⊙O的弦,半径OA=20cm,∠AOB=120°,求线段AB的长.考点:垂径定理,解直角三角形
专题:计算题
分析:作OD⊥AB交AB于点D根据垂径定理得AD=BD,由OA=OB得∠A=∠B,而∠AOB=120°,根据三角形内角和定理得到∠A=30°,在Rt△AOD中,根据含30度的直角三角形三边的关系得OD=
OA=10,AD=
OD=10
,所以AB=2AD=20
cm.
| 1 |
| 2 |
| 3 |
| 3 |
| 3 |
解答:解:作OD⊥AB交AB于点D, 如图,则AD=BD,
如图,则AD=BD,
∵OA=OB,
∴∠A=∠B,
而∠AOB=120°,
∴∠A=30°,
在Rt△AOD中,OD=
OA=
×20=10,
AD=
OD=10
,
∴AB=2AD=20
(cm).
 如图,则AD=BD,
如图,则AD=BD,∵OA=OB,
∴∠A=∠B,
而∠AOB=120°,
∴∠A=30°,
在Rt△AOD中,OD=
| 1 |
| 2 |
| 1 |
| 2 |
AD=
| 3 |
| 3 |
∴AB=2AD=20
| 3 |
点评:本题考查了垂径定理:平分弦的直径平分这条弦,并且平分弦所对的两条弧.也考查了含30度的直角三角形三边的关系.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 如图,已知:a∥b,∠3=137°,则∠2=
如图,已知:a∥b,∠3=137°,则∠2=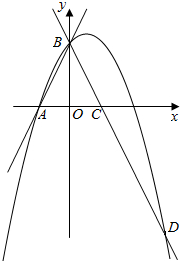 如图,直线y=2x+2与x轴交于点A,与y轴交于点B,把△AOB沿y轴翻折,点A落到点C,过点B的抛物线y=-x2+bx+c与直线BC交于点D(3,-4).
如图,直线y=2x+2与x轴交于点A,与y轴交于点B,把△AOB沿y轴翻折,点A落到点C,过点B的抛物线y=-x2+bx+c与直线BC交于点D(3,-4).