题目内容

9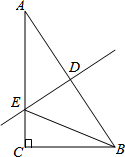．如图，Rt△ABC中，∠C=90°，AB的垂直平分线DE交AC于点E，连接BE，若∠A=40°，则∠CBE的度数为（　　）
A．10°B．15°C．20°D．25°

分析 根据线段的垂直平分线的性质得到EA=EB，得到∠ABE=∠A=40°，根据三角形的外角的性质求出∠CEB，根据三角形内角和定理计算即可．

解答 解：∵DE是AB的垂直平分线，
∴EA=EB，
∴∠ABE=∠A=40°，
∴∠CEB=80°，
∵∠C=90°，
∴∠CBE=10°，
故选：A．

点评 本题考查的是线段的垂直平分线的性质，掌握线段的垂直平分线上的点到线段的两个端点的距离相等是解题的关键．

练习册系列答案
相关题目
19．如图所示，在矩形ABCD中，AB=10，BC=6，点E、F在DC边上，连接AF、BE交于点P，若EF=$\frac{1}{2}$DC，则图中阴影部分的面积为（　　）
A．50B．45C．40D．35
20．下列计算正确的是（　　）
A．$\sqrt{（-2）^{2}}$=-2B．$\sqrt{9}$=±3C．$\root{3}{-8}$=-2D．$\sqrt{25}$-$\sqrt{16}$=$\sqrt{9}$
17．以下命题中是真命题的是（　　）
A．内错角相等
B．相等的角是对顶角
C．两个角的和等于平角时，这两个角互为补角
D．两个锐角的和是锐角
4．某校从初二年级抽出40名女生的身高数据，分组整理出如下频数分布表：
分组/cm频    数频    率
145～15020.05
150～155a0.15
155～160140.35
160～165bc
165～17060.15
合计401.00
表中a，b，c分别是（　　）
A．6，12，0.30B．6，10，0.25C．8，12，0.30D．6，12，0.24
14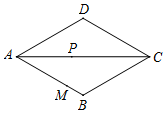．如图，菱形ABCD中，∠DAB=60°，点P是对角线AC上的动点，点M在边AB上，且AM=4，则点P到点M与到边AB的距离之和的最小值是（　　）
A．4B．2$\sqrt{3}$C．2$+\sqrt{3}$D．$\frac{8}{3}$$\sqrt{3}$
1．下列事件中，随机事件是（　　）
A．经过有交通信号灯的路口，遇到红灯
B．实心铁球投入水中会沉入水底
C．一滴花生油滴入水中，油会浮在水面
D．两负数的和为正数
18．如图，多边形ABCDEF与AGHEMN都是正六边形，则∠FAN的度数为（　　）
A．15°B．20°C．30°D．45°
19．下列各组数据中的三个数作为三角形的边长，其中能构成直角三角形的是（　　）
A．1，2，3B．$\sqrt{2}$，$\sqrt{3}$，$\sqrt{5}$C．3，5，7D．5，7，9

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网