题目内容
14.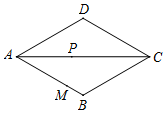 如图,菱形ABCD中,∠DAB=60°,点P是对角线AC上的动点,点M在边AB上,且AM=4,则点P到点M与到边AB的距离之和的最小值是( )
如图,菱形ABCD中,∠DAB=60°,点P是对角线AC上的动点,点M在边AB上,且AM=4,则点P到点M与到边AB的距离之和的最小值是( )| A. | 4 | B. | 2$\sqrt{3}$ | C. | 2$+\sqrt{3}$ | D. | $\frac{8}{3}$$\sqrt{3}$ |
分析 作M关于AC的对称点M′,得到AM′=AM=4,过M′作M′N⊥AB交AC于P,解直角三角形即可得到结论.
解答  解:作M关于AC的对称点M′,
解:作M关于AC的对称点M′,
则M′在AD上,且AM′=AM=4,
过M′作M′N⊥AB交AC于P,
则此时,点P到点M与到边AB的距离之和的最小,且等于M′N,
∵∠DAB=60°,
∴△AMM′是等边三角形,
∴M′N=$\frac{\sqrt{3}}{2}$AM′=2$\sqrt{3}$,
即点P到点M与到边AB的距离之和的最小值是2$\sqrt{3}$,
故选B.
点评 本题考查的是最短线路问题及菱形的性质,由菱形的性质得出△AMM′是等边三角形是解答此题的关键.

练习册系列答案
相关题目
9.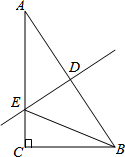 如图,Rt△ABC中,∠C=90°,AB的垂直平分线DE交AC于点E,连接BE,若∠A=40°,则∠CBE的度数为( )
如图,Rt△ABC中,∠C=90°,AB的垂直平分线DE交AC于点E,连接BE,若∠A=40°,则∠CBE的度数为( )
 如图,Rt△ABC中,∠C=90°,AB的垂直平分线DE交AC于点E,连接BE,若∠A=40°,则∠CBE的度数为( )
如图,Rt△ABC中,∠C=90°,AB的垂直平分线DE交AC于点E,连接BE,若∠A=40°,则∠CBE的度数为( )| A. | 10° | B. | 15° | C. | 20° | D. | 25° |
19.以下列所给线段长为三边,能构成三角形的是( )
| A. | 1cm、2cm、3cm | B. | 3cm、4cm、6cm | C. | 1cm、1cm、3cm | D. | 2cm、3cm、7cm |
6.某市初中毕业生进行了一项技能测试,有4万名考生的得分都是不小于70的两位数,从中随机抽取3000个数据,统计如下表:
请根据表格中的信息,估计这4万个数据的平均数约为( )
| 数据x | 70≤x≤79 | 80≤x≤89 | 90≤x≤99 |
| 个数 | 800 | 1300 | 900 |
| 平均数 | 78 | 85 | 92 |
| A. | 92 | B. | 85 | C. | 83 | D. | 78 |
3.某商场“五•一”期间做促销活动,一件600元的电器第一次降价后销售较慢,于是又进行第二次降价,第二次降价的百分率是第一次的2倍,结果以432元的价格迅速销售一空,设第一次降价的百分率为x,根据题意,下面所列方程正确的是( )
| A. | 600x•2x=432 | B. | 600(1-x)•2x=432 | C. | 600(1-x)(1-2x)=432 | D. | 600(1-x)(1-x2)=432 |
4.当a≠0时,下列运算正确的是( )
| A. | a0=0 | B. | ${a^{-2}}=-\frac{1}{a^2}$ | C. | (-a)4=-a4 | D. | a-2÷a-3=a |
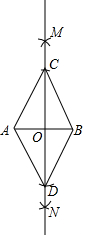 小明在白纸上作一个菱形,他按如下步骤:
小明在白纸上作一个菱形,他按如下步骤: