题目内容
5.如图,下列正方形网格的每个小正方形的边长均为1,⊙O的半径为n≥8$\frac{1}{3}$.规定:顶点既在圆上又是正方形格点的直角三角形称为“圆格三角形”,请按下列要求各画一个“圆格三角形”,并用阴影表示出来.
分析 (1)以直径为斜边,直角边分别为2和6的圆内接直角三角形满足要求;
(2)以直径为斜边,直角边分别为2$\sqrt{2}$和4$\sqrt{2}$的圆内接直角三角形满足要求;
(3)以直径为斜边,直角边为2$\sqrt{5}$的圆内接等腰直角三角形满足要求.
解答 解:(1)如图1所示,△ABC即为所求三角形,其中AC=2,BC=6;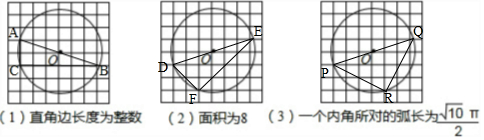
(2)如图2所示,△DEF即为所求作三角形,其中DF=2$\sqrt{2}$,EF=4$\sqrt{2}$,
则其面积为$\frac{1}{2}$×2$\sqrt{2}$×4$\sqrt{2}$=8;
(3)如图3所示,△PQR即为所求作三角形,其中PR=QR,∠PRQ=90°,
∵PQ=$\sqrt{{6}^{2}+{2}^{2}}$=2$\sqrt{10}$,
∴∠PRQ所对弧长为$\frac{90•π•\sqrt{10}}{180}$=$\frac{\sqrt{10}}{2}$π.
点评 本题主要考查了圆周角定理的推论、勾股定理、弧长公式等知识点,理解新定义是解题的根本,熟练掌握直径所对圆周角是直角是解题的关键.

练习册系列答案
相关题目
10.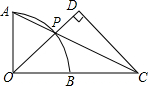 如图,点O为弧AB所在圆的圆心,OA⊥OB,点P在弧AB上,AP的延长线与OB的延长线交于点C,过点C作CD⊥OP于D.若OB=BC=1,则PD的长为( )
如图,点O为弧AB所在圆的圆心,OA⊥OB,点P在弧AB上,AP的延长线与OB的延长线交于点C,过点C作CD⊥OP于D.若OB=BC=1,则PD的长为( )
 如图,点O为弧AB所在圆的圆心,OA⊥OB,点P在弧AB上,AP的延长线与OB的延长线交于点C,过点C作CD⊥OP于D.若OB=BC=1,则PD的长为( )
如图,点O为弧AB所在圆的圆心,OA⊥OB,点P在弧AB上,AP的延长线与OB的延长线交于点C,过点C作CD⊥OP于D.若OB=BC=1,则PD的长为( )| A. | $\frac{2}{5}$ | B. | $\frac{1}{2}$ | C. | $\frac{3}{5}$ | D. | $\frac{4}{5}$ |

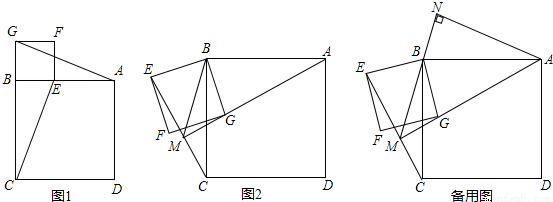
 AE2;④∠DFE=2∠DAC ;⑤若连接CH,则CH∥EF.其中正确的个数为( )
AE2;④∠DFE=2∠DAC ;⑤若连接CH,则CH∥EF.其中正确的个数为( )
 的倒数是( )
的倒数是( ) B.
B.  C.
C.  D.
D. 
 如图,已知△ABD≌△ACD,那么AD与BC有怎样的位置关系?为什么?
如图,已知△ABD≌△ACD,那么AD与BC有怎样的位置关系?为什么?