题目内容
7.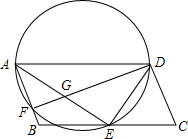 如图,在平行四边形ABCD中,E为BC边上的一点,且AE与DE分别平分∠BAD和∠ADC
如图,在平行四边形ABCD中,E为BC边上的一点,且AE与DE分别平分∠BAD和∠ADC(1)求证:AE⊥DE;
(2)设以AD为直径的半圆交AB于F,连接DF交AE于G,已知CD=10,AE=16,求$\frac{FG}{AE}$的值.
分析 (1)由四边形ABCD是?,可知AB∥CD,那么就有∠BAD+∠ADC=180°,又AE、DE是∠BAD、∠ADC的角平分线,容易得出∠DAE+∠ADE=90°,即AE⊥DE;
(2)由于AD∥BC,AE是角平分线,容易得∠BAE=∠BEA,那么AB=BE=CD=10,同理有CE=CD=10,容易得出AD=BC=BE+CE=20.在Rt△ADE中,利用勾股定理可求DE,由于AD是直径,所以tan∠FAG=$\frac{FG}{AF}$,而∠FAG=∠DAE,于是$\frac{FG}{AF}$=$\frac{DE}{AE}$,即可求.
解答 (1)证明:在平行四边形ABCD中,AB∥CD,
∴∠BAD+∠ADC=180°.
又∵AE、DE平分∠BAD、∠ADC,
∴∠DAE+∠ADE=90°,
∴∠AED=90°,
∴AE⊥DE.
(2)解:在平行四边形ABCD中,AD∥BC,AB=CD=5,AD=BC,
∴∠DAE=∠BEA.
又∵∠DAE=∠BAE,
∴∠BEA=∠BAE,
∴BE=AB=10.
同理EC=CD=10.
∴AD=BC=BE+EC=20.
在Rt△AED中,DE=$\sqrt{A{D}^{2}-A{E}^{2}}$=$\sqrt{2{0}^{2}-1{6}^{2}}$=12.
又∵AE是∠BAD的角平分线,
∴∠FAG=∠DAE.
∵AD是直径,
∴∠AFD=90°,
∴tan∠FAG=$\frac{FG}{AF}$,
∴$\frac{FG}{AF}$=tan∠DAE=$\frac{DE}{AE}$=$\frac{3}{4}$.
点评 本题考查了相似三角形的判定和性质,勾股定理,平行四边形的性质,角平分线的定义,熟练掌握各定理是解题的关键.

 寒假大串联黄山书社系列答案
寒假大串联黄山书社系列答案 寒假创新型自主学习第三学期寒假衔接系列答案
寒假创新型自主学习第三学期寒假衔接系列答案| A. | 40π | B. | 20π | C. | 4π | D. | 2π |
| A. | x(15-x) | B. | x(30-x) | C. | x(30-2x) | D. | x(15+x) |
 如图,在平行四边形ABCD中,E是AB的中点,CE和BD交于点O,计算点O到AB与CD边的距离之比.
如图,在平行四边形ABCD中,E是AB的中点,CE和BD交于点O,计算点O到AB与CD边的距离之比.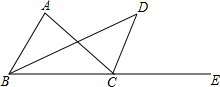 如图所示,已知BD为△ABC的角平分线,CD为△ABC外角∠ACE的平分线,且与BD交于点D;
如图所示,已知BD为△ABC的角平分线,CD为△ABC外角∠ACE的平分线,且与BD交于点D;