Question

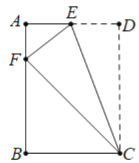
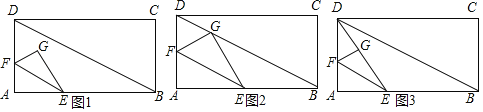
【题目】图1是一种推磨工具模型，图2是它的示意图，已知AB⊥PQ，AP＝AQ＝3dm，AB＝12dm，点A在中轴线l上运动，点B在以O为圆心，OB长为半径的圆上运动，且OB＝4dm．

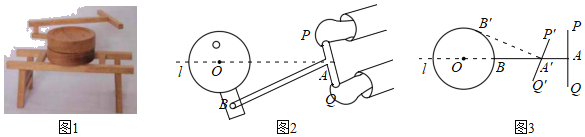
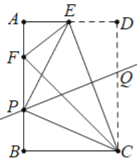
（1）如图3，当点B按逆时针方向运动到B′时，A′B′与⊙O相切，则AA′＝__dm．

（2）在点B的运动过程中，点P与点O之间的最短距离为__dm．

Answer 1

【答案】（16﹣4） （3﹣4）

【解析】

（1）根据A′A＝OA﹣OA′＝AB+OB﹣OA，即可求解；

（2）当B、O、P三点共线时，OP的距离最短，即可求解．

解：（1）A′A＝OA﹣OA′＝AB+OB﹣OA＝12+4﹣＝16﹣＝16﹣4，

故答案为：（16﹣4）；

（2）当B、O、P三点共线时，OP的距离最短，

则OP＝BP﹣OB＝＝-4＝3﹣4（dm），

故答案为：（3﹣4）．