Question

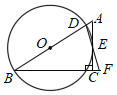
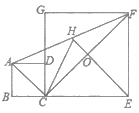
【题目】如图，在矩形ABCD中，E是边AD上的一点，将△CDE沿CE折叠得到△CFE，点F恰好落在边AB上．

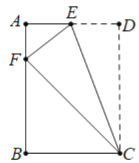
（1）证明：△AEF∽△BFC．

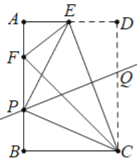
（2）若AB=，BC=1，作线段CE的中垂线，交AB于点P，交CD于点Q，连结PE，PC．

①求线段DQ的长．

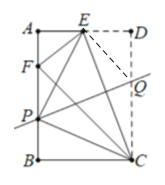
②试判断△PCE的形状，并说明理由．

Answer 1

【答案】（1）详见解析；（2）2-；（3）等腰直角三角形．

【解析】

（1）根据折叠的性质知，从而得出，转化得到相似；

（2）连接EQ，根据AB=，BC=1计算出BF的长度，从而判断都是等腰直角三角形，算出AF、DE的长度，再根据PQ是CE的垂直平分线得出EQ=CQ，设，则，解直角三角形算出x即可；

（3）设，则，根据利用勾股定理建立等量关系解出再证明全等即可．

解：（1）∵将△CDE沿CE折叠得到△CFE

∴

∴

又∵

∴

∴△AEF∽△BFC

（2）①连接EQ，PQ是CE的中垂线，如图：

∵AB=，BC=1，将△CDE沿CE折叠得到△CFE，四边形ABCD是矩形

∴

∴都是等腰直角三角形

∴

设，则，在直角三角形DEQ中：

，解得：

故DQ的长为；

②设，则，PQ是CE的中垂线

∴

∴即

解得：

∴

又∵

∴△APE≌△BCP

∴即

∴△PCE是等腰直角三角形．