Question

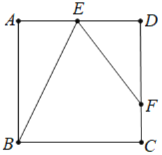
【题目】正方形ABCD中，E为AD的中点，以E为顶点作∠BEF=∠EBC，EF交CD于点F．

（1）求tan∠BEF；

（2）求DF：CF的值．

Answer 1

【答案】（1）2；（2）2．

【解析】

（1）先求得tan∠AEB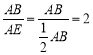＝，再证得∠BEF＝∠AEB，即可求得答案；

（2）设AB＝a，则AE＝DE＝a，过点B作BG⊥EF于G，连接BF，推出△ABE≌△GBE，则AB＝BG＝a，AE＝EG＝a，证出Rt△BGF≌Rt△BCF，得到GF＝CF，根据勾股定理即可得到结果．

解：（1）∵在正方形ABCD中，

∴AD∥BC，∠A＝90°，AB＝AD，

∵E为AD的中点，

∴AE＝AD＝AB

∴在Rt△ABE中，tan∠AEB＝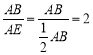

∵AD∥BC，

∴∠EBC＝∠AEB，

∵∠BEF＝∠EBC，

∴∠BEF＝∠AEB，

∴tan∠BEF＝tan∠AEB＝2；

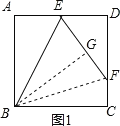
（2）如图1，设AB＝a，则AE＝DE＝a，

过点B作BG⊥EF于G，连接BF，

∵∠FEB＝∠EBC，AD∥BC，∠AEB＝∠EBC，

∴∠AEB＝∠BEF，

在△ABE与△GBE中

，

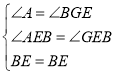∴△ABE≌△GBE，

∴AB＝BG＝a，AE＝EG＝a，

在Rt△BGF与Rt△BCF中

，

∴Rt△BGF≌Rt△BCF，

∴GF＝CF，

设DF＝b，则EF＝，

∴GF＝CF＝EF﹣EG＝﹣a＝a﹣b，

∴a＝，CF＝a﹣b＝b，

∴DF：CF＝b：b＝2．