题目内容
18.如图,△ABC和△ADE为等腰直角三角形,其中∠BAC=∠DAE=90°,AB=AC,AD=AE,将△ADE绕A点旋转至如图的位置(1)判断线段BD和CE的关系,并予以证明;
(2)分别取BD、CE的中点M、N,连AM、AN,判断线段AM、AN的关系,并予以证明.
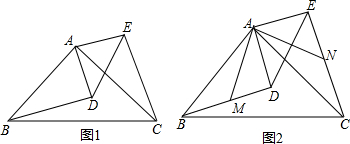
分析 (1)利用等式的性质得出∠BAD=∠CAE,再利用SAS证明△BAD与△CAE全等,进而得出BD=CE;
(2)利用(1)的证明得出BM=CN,∠ABM=∠ACN,进而证明△ABM与△ACN全等即可.
解答 解:(1)相等关系,理由如下:
∵∠BAC=∠DAE=90°,
∴∠BAC-∠DAC=∠DAE-∠DAC,
∴∠BAD=∠CAE,
在△BAD与△CAE中,
$\left\{\begin{array}{l}{AB=AC}\\{∠BAD=∠CAE}\\{AD=AE}\end{array}\right.$,
∴△BAD≌△CAE(SAS),
∴BD=CE;
(2)相等关系,理由如下:
∵△BAD≌△CAE,
∴BD=CE,∠ABM=∠ACN,
∵BD、CE的中点M、N,
∴BM=CN,
在△ABM与△ACN中,
$\left\{\begin{array}{l}{AB=BC}\\{∠ABM=∠ACN}\\{BM=CN}\end{array}\right.$,
∴△ABM≌△ACN(SAS),
∴AM=AN.
点评 此题考查全等三角形灯泡的和性质,关键是利用等式的性质得出∠BAD=∠CAE,再利用SAS证明△BAD与△CAE全等.

练习册系列答案
相关题目
7.下列说法不正确的是( )
| A. | 0的平方根是0 | |
| B. | -22的平方根是±2 | |
| C. | 非负数的平方根是互为相反数 | |
| D. | 一个正数的算术平方根一定大于这个数的相反数 |
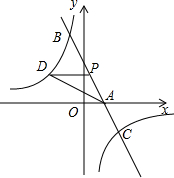 如图,已知一次函数y1=kx+b的图象与x轴相交于点A,与反比例函数y2=$\frac{c}{x}$的图象相交于B(-1,5),C($\frac{5}{2}$,d)两点,点M是y轴上一动点,点P(m,n)是一次函数y=kx+b的图象上的动点.
如图,已知一次函数y1=kx+b的图象与x轴相交于点A,与反比例函数y2=$\frac{c}{x}$的图象相交于B(-1,5),C($\frac{5}{2}$,d)两点,点M是y轴上一动点,点P(m,n)是一次函数y=kx+b的图象上的动点.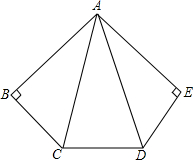 如图,AB⊥BC,AE⊥ED,AB=AE,∠ACD=∠ADC,求证:BC=ED.
如图,AB⊥BC,AE⊥ED,AB=AE,∠ACD=∠ADC,求证:BC=ED.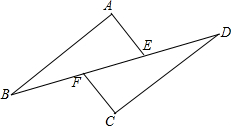 如图,AB∥CD,AE∥CF,BF=DE,试找出图中其他的相等关系,并给出证明.
如图,AB∥CD,AE∥CF,BF=DE,试找出图中其他的相等关系,并给出证明. 如图,已知△ABC和△ABD,∠CAB=∠DBA=90°,BC=5,BD=8,∠CBD=2∠ADB,则AD的长为4$\sqrt{5}$.
如图,已知△ABC和△ABD,∠CAB=∠DBA=90°,BC=5,BD=8,∠CBD=2∠ADB,则AD的长为4$\sqrt{5}$. 如图,正方形ABCD,点E是对角线AC上一点,连接BE,过E作EF⊥BE,EF交CD于F,若AE=2$\sqrt{2}$,CF=5,则正方形ABCD的面积为81.
如图,正方形ABCD,点E是对角线AC上一点,连接BE,过E作EF⊥BE,EF交CD于F,若AE=2$\sqrt{2}$,CF=5,则正方形ABCD的面积为81.