题目内容
已知梯形ABCD的中位线长为4.5，AC、BD交于点O，且BD平分∠ABC，CA平分∠BCD，| AO |
| OC |
| 3 |
| 7 |
考点：梯形中位线定理
专题：
分析：先由梯形ABCD的中位线长为4.5，根据梯形的中位线定理可得AD+BC=2×4.5=9，由AD∥BC，根据平行线分线段成比例定理得到
=
=
，那么AD=
，BC=
．再由角平分线定义及平行线的性质得出∠ABD=∠DBC=∠ADB，根据等角对等边得出AD=AB=
，同理可得AD=DC=
，然后根据梯形ABCD的周长=AD+BC+AB+CD，将数值代入计算即可．
| AD |
| BC |
| AO |
| OC |
| 3 |
| 7 |
| 27 |
| 10 |
| 63 |
| 10 |
| 27 |
| 10 |
| 27 |
| 10 |
解答：解：∵梯形ABCD的中位线长为4.5，
∴AD+BC=2×4.5=9．
∵AD∥BC，
∴
=
=
，
∴AD=
，BC=
．
∵BD平分∠ABC，
∴∠ABD=∠DBC，
∵AD∥BC，
∴∠ADB=∠DBC，
∴∠ABD=∠ADB，
∴AD=AB=
，
同理可得AD=DC=
，
∴梯形ABCD的周长=AD+BC+AB+CD=9+
×2=
．
∴AD+BC=2×4.5=9．
∵AD∥BC，
∴
| AD |
| BC |
| AO |
| OC |
| 3 |
| 7 |
∴AD=
| 27 |
| 10 |
| 63 |
| 10 |
∵BD平分∠ABC，
∴∠ABD=∠DBC，
∵AD∥BC，
∴∠ADB=∠DBC，
∴∠ABD=∠ADB，
∴AD=AB=
| 27 |
| 10 |
同理可得AD=DC=
| 27 |
| 10 |
∴梯形ABCD的周长=AD+BC+AB+CD=9+
| 27 |
| 10 |
| 72 |
| 5 |
点评：本题考查了梯形中位线定理：梯形的中位线平行于两底，并且等于两底和的一半．同时考查了平行线分线段成比例定理，角平分线定义，平行线的性质，等腰三角形的判定，梯形的周长，难度适中．
练习册系列答案
相关题目
将直线y=x平移，使得它经过点（-2，0），则平移后的直线为（ ）
| A、y=x-2 |
| B、y=x+1 |
| C、y=-x-2 |
| D、y=x+2 |
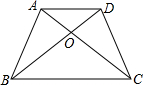如图，在四边形ABCD中，AC与BD相交于点O，如果△ABO≌△DCO，试在图中再找出一对全等三角形，并加以证明．