题目内容
18. 探索与证明
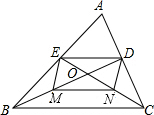
探索与证明如图,在△ABC中,BD、CE分别是边AC、AB上的中线,BD与CE相交于点O,M、N分别是BO、CO的中点,顺次连接E、M、N、D四点.
(1)求证:EMND是平行四边形;
(2)探索:BC边上的中线是否过点O?为什么?
分析 (1)由中位线定理,可得ED∥BC,MN∥BC,且都等于边长BC的一半.分析到此,此题证明即可.
(2)BC边上的中线过点O,连接DE.根据三角形的中位线定理,得DF∥BA,DF=$\frac{1}{2}$BA.根据平行得到三角形MDF相似于三角形MBA,再根据相似三角形的对应边的比相等即可求解.
解答 (1)证明:△ABC的边AC、AB上的中线BD、CE相交于点O,M、N分别是BO、CO的中点,
∴ED∥BC且ED=$\frac{1}{2}$BC,
MN∥BC且MN=$\frac{1}{2}$BC,
∴ED∥MN且ED=MN,
∴四边形MNDE是平行四边形.
(2)BC边上的中线过点O,理由如下:
作BC边上的中线AF,交BD于M,连接DF,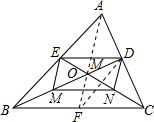
∵BD、AF是边AC、BC上的中线,
∴DF∥BA,DF=$\frac{1}{2}$BA.
∴△MDF∽△MBA,
∴$\frac{DM}{BM}=\frac{FM}{AM}=\frac{DF}{AB}$=$\frac{1}{2}$,
即BD=3DM,
∵BO=$\frac{2}{3}$BD,
∴O和M重合,
即BC边上的中线一定过点O.
点评 此题主要考查了平行四边形的判定,三角形的中位线定理,关键是掌握三角形的中位线平行于第三边,并且等于第三边的一半.

练习册系列答案
相关题目
9.2010年10月31日晚,中国2010上海世博会正式落下帷幕.据官网统计,累计参观人数超过73000 000人次,将73000 000用科学记数法表示应为( )
| A. | 0.73×108 | B. | 7.3×108 | C. | 7.3×107 | D. | 73×106 |
6.某学校要招聘一名教师,分笔试和面试两次考试,笔试、面试和最后得分的满分均为100分,竞聘教师的最后得分按笔试成绩:面试成绩=3:2的比例计算.在这次招聘考试中,某竞聘教师的笔试成绩为90分,面试成绩为80分,则该竞聘教师的最后成绩是( )
| A. | 43分 | B. | 85分 | C. | 86分 | D. | 170分 |
3.若a与2互为相反数,则|a+2|等于( )
| A. | 2 | B. | -2 | C. | 0 | D. | -1 |
15.已知正比例函数y=(2m+3)x的图象上两点A(x1,y1)和 A(x2,y2),当x1<x2时y1>y2,则m的取值范围是( )
| A. | $m<-\frac{3}{2}$ | B. | $m>-\frac{3}{2}$ | C. | $0<m<\frac{3}{2}$ | D. | m<0 |
 如图,图中有几个三角形?把它们表示出来,并写出∠B的对边.
如图,图中有几个三角形?把它们表示出来,并写出∠B的对边.