题目内容
15.已知正比例函数y=(2m+3)x的图象上两点A(x1,y1)和 A(x2,y2),当x1<x2时y1>y2,则m的取值范围是( )| A. | $m<-\frac{3}{2}$ | B. | $m>-\frac{3}{2}$ | C. | $0<m<\frac{3}{2}$ | D. | m<0 |
分析 由题目所给信息“当x1<x2时 y1>y2”可以知道,y随x的增大而减小,则由一次函数性质可以知道应有:2m+3<0.
解答 解:∵正比例函数y=(2m+3)x的图象经过点A(x1,y1)和点B(x2,y2),当x1<x2时 y1>y2时,
∴正比例函数y=(2m+3)x的图象是y随x的增大而减小,
∴2m+3<0,
解得:m$<-\frac{3}{2}$
故选A
点评 本题考查了一次函数图象上点的坐标特征.准确理解一次函数图象的性质,确定y随x的变化情况是解题的关键.

练习册系列答案
相关题目
20.在实数:-0.3,$\sqrt{1}$,2.010010001…(0的个数依次递增),4.$\stackrel{••}{21}$,2π,$\frac{22}{7}$中,无理数有( )
| A. | 1 | B. | 2个 | C. | 3个 | D. | 4个 |
4.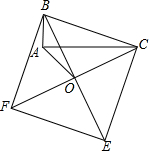 如图,以Rt△ABC的斜边BC为一边在△ABC的同侧作正方形BCEF,对角线交于点O,连结AO,如果AB=4,AO=4$\sqrt{2}$,那么AC的长等于( )
如图,以Rt△ABC的斜边BC为一边在△ABC的同侧作正方形BCEF,对角线交于点O,连结AO,如果AB=4,AO=4$\sqrt{2}$,那么AC的长等于( )
 如图,以Rt△ABC的斜边BC为一边在△ABC的同侧作正方形BCEF,对角线交于点O,连结AO,如果AB=4,AO=4$\sqrt{2}$,那么AC的长等于( )
如图,以Rt△ABC的斜边BC为一边在△ABC的同侧作正方形BCEF,对角线交于点O,连结AO,如果AB=4,AO=4$\sqrt{2}$,那么AC的长等于( )| A. | 12 | B. | 16 | C. | 4$\sqrt{3}$ | D. | 8$\sqrt{3}$ |
 探索与证明
探索与证明 如图,将Rt△ABC绕点A逆时针旋转34°,得到Rt△AB′C′,点C′恰好落在斜边AB上,连接BB′,则∠BB′C′的度数为17°.
如图,将Rt△ABC绕点A逆时针旋转34°,得到Rt△AB′C′,点C′恰好落在斜边AB上,连接BB′,则∠BB′C′的度数为17°.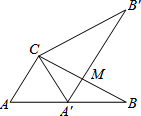 如图,△ABC中,∠ACB=90°,∠B=30°,BC=6,三角板绕C逆时针旋转,当点A的对应点A′落在AB边上时即停止转动,则BM的长为3.
如图,△ABC中,∠ACB=90°,∠B=30°,BC=6,三角板绕C逆时针旋转,当点A的对应点A′落在AB边上时即停止转动,则BM的长为3.