题目内容
如图，在平行四边形ABCD中，AC与BD相交于点O，E为OD的中点，连接AE并延长交DC于点F，则S△DEF：S△ADE的值为 （ ）| A、1：4 | B、1：3 |
| C、2：3 | D、1：2 |
考点：相似三角形的判定与性质,平行四边形的性质
专题：计算题,几何图形问题
分析：过E作EM⊥CD，反向延长交AB于点N，根据△DEF∽△BEA，即可求得ME与MN的比值，则△DEF和△DAF的面积即可求解，进而求得所求．
解答：
解：过E作EM⊥CD，反向延长交AB于点N，
∵平行四边形ABCD中，OB=OD，E为OD的中点，
∴BE=3DE，CD∥AB，
∴△DEF∽△BEA，
∴
=
=
，
∴
=
，
∴
=
，
∴S△DEF：S△ADE=1：3．
故选B．
解：过E作EM⊥CD，反向延长交AB于点N，∵平行四边形ABCD中，OB=OD，E为OD的中点，
∴BE=3DE，CD∥AB，
∴△DEF∽△BEA，
∴
| ME |
| EN |
| DE |
| BE |
| 1 |
| 3 |
∴
| ME |
| MN |
| 1 |
| 4 |
∴
| S△DEF |
| S△DAF |
| 1 |
| 4 |
∴S△DEF：S△ADE=1：3．
故选B．
点评：本题考查了相似三角形的判定与性质，以及三角形的面积的计算，正确求得ME与MN的比值是关键．
练习册系列答案
津桥教育暑假拔高衔接广东人民出版社系列答案
波波熊暑假作业江西人民出版社系列答案
学而优暑期衔接南京大学出版社系列答案
相关题目
二元一次方程3a+b=9在正整数范围内的解的个数是（ ）
| A、1个 | B、2个 | C、3个 | D、4个 |
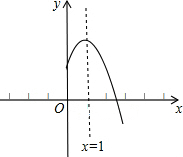二次函数y=ax2+bx+c（a，b，c是常数，a≠0）图象的对称轴是直线x=1，其图象的一部分如图，对于下列说法：①abc＜0；②a-b+c＜0；③3a+c＜0；④当-1＜x＜3时，y＞0．
其中正确的是（ ）
| A、①、② | B、①、③ |
| C、①、②、③ | D、①、②、④ |
等边△ABC在数轴上的位置如图，点A、C对应的数分别为0和-1，若△ABC绕顶点沿顺时针方向在数轴上连续翻转，翻转1次后，点B所对应的数为1，则连续翻转2009次后，点B（ ）
| A、不对应任何数 |
| B、对应的数是2007 |
| C、对应的数是2008 |
| D、对应的数是2009 |
将式子a
（a＜0）中根号外的因式移到根号里面，其中正确的是（ ）
-
|
A、
| ||
B、-
| ||
C、
| ||
D、-
|
如图，DE是△ABC的中位线，延长DE至F使EF=DE，连接CF，则CF：AB的值为（ ）| A、1：3 | B、2：3 |
| C、3：4 | D、1：2 |
一次函数y=2012x-2012的图象不经过的象限是（ ）
| A、第一象限 | B、第二象限 |
| C、第三象限 | D、第四象限 |