题目内容
12.已知:关于x的一元二次方程x2-(2m-3)x+m2-5m+2=0有两个不相等的实数根.(1)求m的取值范围;
(2)若10<m<21,是否存在整数m,使方程有两个整数根,若存在求出m的值;若不存在请说明理由.
分析 (1)由题意知根的判别式的值大于0,据此解关于m的不等式可得答案;
(2)解方程得出方程的解为 $x=\frac{{(2m-3)±\sqrt{8m+1}}}{2}$,根据10<m<21,m为整数得81<8m+1<169,即9<$\sqrt{8m+1}$<13,由方程有两个整数根知$\sqrt{8m+1}$=10或11或12,继而得出整数m的值.
解答 解:(1)△=[-(2m-3)]2-4(m2-5m+2)=8m+1,
由8m+1>0得$m>-\frac{1}{8}$;
(2)存在整数m,使方程有两个整数根,
原因:方程解为 $x=\frac{{(2m-3)±\sqrt{8m+1}}}{2}$,
∵10<m<21,m为整数,
∴81<8m+1<169 且为整数,
∴9<$\sqrt{8m+1}$<13,
又∵方程有两个整数根,
∴$\sqrt{8m+1}$=10或11或12,
∴$m=\frac{99}{8}或15或\frac{11}{8}$,
∴整数m=15,
当m=15时,x1=19,x2=8符合题意.
点评 本题主要考查一元二次方程根的判别式,一元二次方程ax2+bx+c=0(a≠0)的根与△=b2-4ac有如下关系:
①当△>0时,方程有两个不相等的两个实数根;②当△=0时,方程有两个相等的两个实数根;③当△<0时,方程无实数根.

练习册系列答案
相关题目
2.下列各组线段中,能组成比例线段的是( )
| A. | 0.1,0.2,0.3,0.4 | B. | 0.2,0.8,12,30 | C. | 1,3,4,6 | D. | 12,16,45,60 |
3.若关于x的一元二次方程(m-2)x2+5x+m2-3m+2=0有一根为0,则另一根等于( )
| A. | 0 | B. | 1 | C. | 2 | D. | 5 |
1.如图,已知点E,D,F分别为△ABC三边上的点,下列条件中能判断EF∥BC的是( )
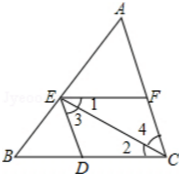

| A. | ∠1=∠3 | B. | ∠3=∠A | C. | ∠1=∠2 | D. | ∠1=∠A |
 由于持续高温和连日无雨,某水库的需水量随着时间的增加而减少,干旱持续时间t(天)与蓄水量v(万立方米)的关系如图所示.请你根据图象所提供的信息回答下列问题.
由于持续高温和连日无雨,某水库的需水量随着时间的增加而减少,干旱持续时间t(天)与蓄水量v(万立方米)的关系如图所示.请你根据图象所提供的信息回答下列问题.