题目内容
5.△ABC中,BC>AB>AC,∠ACB=50°,点D、点E是射线BA上的两个点,且满足AD=AC,BE=BC,则∠DCE的度数为25°.分析 根据等腰三角形的性质和三角形的内角和得到∠BEC=(180°-∠ABC)÷2,∠ADC=(180°-∠DAC)÷2=∠BAC÷2,由外角的性质得到∠DCE=∠BEC-∠ADC,于是得到结论.
解答 解:点D、点E是射线BA上的两个点,如图,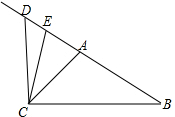
∵BE=BC,∴∠BEC=(180°-∠ABC)÷2,
∵AD=AC,∴∠ADC=(180°-∠DAC)÷2=∠BAC÷2,
∵∠DCE=∠BEC-∠ADC,
∴∠DCE=(180°-∠ABC)÷2-∠BAC÷2=(180°-∠ABC-∠BAC)÷2
=∠ACB÷2=50°÷2=25°,
故答案为:25°.
点评 本题考查了等腰三角形的性质,三角形的内角和,三角形的外角的性质,熟练掌握等腰三角形的性质是解题的关键.

练习册系列答案
 举一反三同步巧讲精练系列答案
举一反三同步巧讲精练系列答案 口算与应用题卡系列答案
口算与应用题卡系列答案
相关题目
13.下列说法正确的是( )
| A. | a一定是正数,-a一定是负数 | B. | -1是最大的负整数 | ||
| C. | 0既没有倒数也没有相反数 | D. | 若a≠b,则a2≠b2 |
20.下列四个“QQ表情”图片中,不是轴对称图形的是( )
| A. |  | B. |  | C. |  | D. |  |
10.下列命题中,真命题的个数为( )
(1)等腰三角形的底角一定是锐角.
(2)三角形两边中垂线的交点到三边的距离相等.
(3)等边三角形是轴对称图形,三条高是其对称轴.
(4)等腰三角形底边上任意一点到两腰的距离之和为定值.
(1)等腰三角形的底角一定是锐角.
(2)三角形两边中垂线的交点到三边的距离相等.
(3)等边三角形是轴对称图形,三条高是其对称轴.
(4)等腰三角形底边上任意一点到两腰的距离之和为定值.
| A. | 0个 | B. | 1个 | C. | 2个 | D. | 3个 |
17.若a=b,那么下列各式不一定成立的是( )
| A. | $a-\frac{1}{3}=b-\frac{1}{3}$ | B. | $-\frac{3}{4}a=-\frac{3}{4}b$ | C. | 3a-1=3b-1 | D. | $\frac{a}{c}=\frac{b}{c}$ |
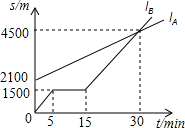 A、B两名同学在一个学校上学,B同学上学的路上经过A同学家.A同学步行,B同学骑自行车,某天,A,B两名同学同时从家出发到学校,如图,lA表示A同学离B同学家的路程sA(m)与行走时间t(min)之间的函数关系图象,lB表示B同学离家的路程sB(m)与行走时间t(min)之间的函数关系图象.
A、B两名同学在一个学校上学,B同学上学的路上经过A同学家.A同学步行,B同学骑自行车,某天,A,B两名同学同时从家出发到学校,如图,lA表示A同学离B同学家的路程sA(m)与行走时间t(min)之间的函数关系图象,lB表示B同学离家的路程sB(m)与行走时间t(min)之间的函数关系图象.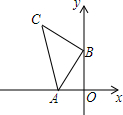 如图,A(-2,0),B(0,4),以B点为直角顶点在第二象限作等腰直角△ABC,则C点坐标为(-4,6).
如图,A(-2,0),B(0,4),以B点为直角顶点在第二象限作等腰直角△ABC,则C点坐标为(-4,6).