题目内容
15.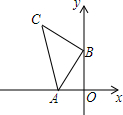 如图,A(-2,0),B(0,4),以B点为直角顶点在第二象限作等腰直角△ABC,则C点坐标为(-4,6).
如图,A(-2,0),B(0,4),以B点为直角顶点在第二象限作等腰直角△ABC,则C点坐标为(-4,6).
分析 作CD⊥y轴于点D,证明△CDB与△BOA全等即可.
解答 解:过点C作CD⊥y轴于点D,如图: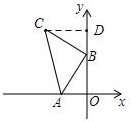
∵△ABC是等腰直角三角形,
∴BC=AB,∠ABC=90°,
∴∠CBD+∠ABO=90°,
∵∠CBD+∠BCD=90°,
∴∠ABO=∠BCD,
在△BCD与△ABO中,
$\left\{\begin{array}{l}{BC=AB}\\{∠BCD=∠ABO}\\{∠CDB=∠BOA}\end{array}\right.$,
∴△BCD≌△ABD(AAS),
∴CD=BO,BD=AO,
∵A(-2,0),B(0,4),
∴AO=2,BO=4,
∴DO=6,
∴C点的坐标为(-4,6).
故答案为:(-4,6).
点评 本题考查全等三角形的判定与性质,是基础题.熟悉全等三角形的判定方法是解答的关键.

练习册系列答案
相关题目
6.将△ABC绕O点顺时针旋转50°得△A1B1C1(A、B分别对应A1、B1),则直线AB与直线A1B1的夹角(锐角)为( )
| A. | 130° | B. | 50° | C. | 40° | D. | 60° |
3. 如图,在△ABC中,已知点D,E,F分别为边BC,AD,CE的中点,且S△ABC=8cm2,则S阴影等于( )
如图,在△ABC中,已知点D,E,F分别为边BC,AD,CE的中点,且S△ABC=8cm2,则S阴影等于( )
 如图,在△ABC中,已知点D,E,F分别为边BC,AD,CE的中点,且S△ABC=8cm2,则S阴影等于( )
如图,在△ABC中,已知点D,E,F分别为边BC,AD,CE的中点,且S△ABC=8cm2,则S阴影等于( )| A. | 4cm2 | B. | 2cm2 | C. | 1cm2 | D. | 6cm2 |
10.下列计算正确的是( )
| A. | $\sqrt{8}-\sqrt{2}=\sqrt{6}$ | B. | $\frac{{\sqrt{27}-\sqrt{12}}}{3}=\sqrt{9}-\sqrt{4}$=1 | C. | $(2-\sqrt{5})(2+\sqrt{5})=1$ | D. | $\frac{{6-\sqrt{2}}}{{\sqrt{2}}}=3\sqrt{2}$-1 |
20.针对关于x的分式方程$\frac{m}{x+6}$=1.下列说法正确的是( )
| A. | 方程的解是x=m-6 | B. | m>6时,方程的解是正数 | ||
| C. | m<6时,方程的解为负数 | D. | 无法确定 |
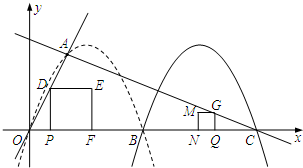 在平面直角坐标系中,抛物线y1=ax2+3x+c经过原点及点A(1,2),与x轴相交于另一点B.
在平面直角坐标系中,抛物线y1=ax2+3x+c经过原点及点A(1,2),与x轴相交于另一点B.