题目内容
4.若a是方程x2-2011x+1=0的一个根,则代数式a2-2012a+$\frac{{a}^{2}+1}{2011}$的值为( )| A. | 1 | B. | 2011 | C. | 0 | D. | -1 |
分析 根据一元二次方程的解的定义得到a2-2011a+1=0,则a2=2011a-1,a2+1=2011a,然后利用整体代入的方法计算代数式a2-2012a+$\frac{{a}^{2}+1}{2011}$的值.
解答 解:∵a是方程x2-2011x+1=0的一个根,
∴a2-2011a+1=0,
∴a2=2011a-1,a2+1=2011a,
∴原式=2011a-1-2012a+$\frac{2011a}{2011}$
=-a-1+a
=-1.
故选D.
点评 本题考查了一元二次方程的解:能使一元二次方程左右两边相等的未知数的值是一元二次方程的解.

练习册系列答案
 阳光同学一线名师全优好卷系列答案
阳光同学一线名师全优好卷系列答案
相关题目
14.对于-3.14,下列说法正确的是( )
| A. | 是负数不是分数 | B. | 是分数不是有理数 | ||
| C. | 是负数也是分数 | D. | 不是分数是有理数 |
15.计算$\frac{1}{8}$×(-8)÷(-$\frac{1}{8}$)结果等于( )
| A. | 8 | B. | -8 | C. | $\frac{1}{8}$ | D. | 1 |
9.下列各式正确的是( )
| A. | $\sqrt{(-2)^{2}}$=-2 | B. | $\sqrt{4}$=±2 | C. | -22=4 | D. | -$\sqrt{9}$=-3 |
16.下面各角能成为某多边形的内角和的是( )
| A. | 430° | B. | 4320° | C. | 4334° | D. | 4360° |
14.已知直角三角形的两条直角边分别是3和4,则它斜边上的中线长为( )
| A. | 2.4 | B. | 2.5 | C. | 3 | D. | 5 |
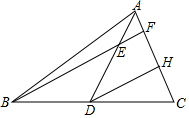 如图,AD为△ABC的中线,AE=$\frac{1}{3}$AD,BE交AC于点F,DH∥BF,则$\frac{AF}{CH}$=$\frac{1}{2}$.
如图,AD为△ABC的中线,AE=$\frac{1}{3}$AD,BE交AC于点F,DH∥BF,则$\frac{AF}{CH}$=$\frac{1}{2}$.