题目内容

16．下面各角能成为某多边形的内角和的是（　　）
A．430°B．4320°C．4334°D．4360°

分析 利用多边形的内角和公式可知，多边形的内角和是180度的倍数，由此即可找出答案．

解答 解：因为多边形的内角和可以表示成（n-2）•180°（n≥3且n是整数），则多边形的内角和是180度的倍数，
在这四个选项中是180的倍数的只有4320度．
故选：B．

点评 本题主要考查了多边形的内角和定理，是需要识记的内容．

练习册系列答案
相关题目
6．对于有理数a，b有下列几种说法，其中正确的个数有（　　）
①若a+b=0，则a与b互为相反数；  
②若a+b＜0，则a与b异号；
③若a与b同号，则a+b＞0；        
④若|a|＞|b|，且a与b同号，则a+b＞0．
A．3个B．2个C．1个D．0个
7．下列说法中正确的是（　　）
A．-a一定是负数B．-|a|一定是负数C．|-a|一定不是负数D．-a2一定是负数
4．若a是方程x2-2011x+1=0的一个根，则代数式a2-2012a+$\frac{{a}^{2}+1}{2011}$的值为（　　）
A．1B．2011C．0D．-1
11．下列数中：$\sqrt{16}$，$\frac{22}{7}$，π，$\root{3}{9}$，3.1415，2.101010…其中无理数有（　　）个．
A．5个B．4个C．3个D．2个
1．如图，点O为△ABC角平分线的交点，点D在CA的延长线上，且BC=CD，AD=AO，若∠BAC=70°，则∠ACB的度数为75°．
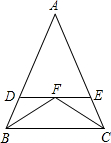8．如图，△ABC中AB=AC，BF、CF分别平分∠ABC、∠ACB，过点F作直线DE∥BC，交AB、AC于D、E，则图中共有等腰三角形（　　）个．
A．6个B．5个C．4个D．3个
5．在平面直角坐标系中，点O是坐标原点，点A的坐标为（0，4），点P是x轴正半轴上一点，AP=2$\sqrt{5}$，点C在第一象限，∠APC=90°，如果△AOP∽△APC，则点C的坐标为（4，1）．
6．如果a＜3，那么|-2|+|a-4|等于（　　）
A．6-aB．a-6C．a-2D．2-a

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网