题目内容
13.多项式ax3-a与多项式x2-2x+1的公因式是x-1.分析 多项式都含有的公共的因式叫做多项式的公因式,据此可将多项式ax3-a先提取公因式、再利用立方差公式分解,将多项式x2-2x+1利用完全平方公式分解,然后找出它们的公因式.
解答 解:∵ax3-a=a(x3-1)=a(x-1)(x2+x+1),x2-2x+1=(x-1)2,
∴多项式ax3-a与多项式x2-2x+1的公因式是(x-1),
故答案为:x-1.
点评 本题主要考查公因式的确定,熟练掌握公因式的定义及确定方法是解题的根本,准确利用提公因式法和公式法将多项式分解是解题的关键.

练习册系列答案
相关题目
8.下列根式中,不能与$\sqrt{3}$合并的是( )
| A. | $\sqrt{\frac{1}{3}}$ | B. | $\frac{3}{{\sqrt{3}}}$ | C. | $\sqrt{\frac{2}{3}}$ | D. | $\sqrt{12}$ |
18.下列各个运算中,能合并成一个根式的是( )
| A. | $\sqrt{12}$-$\sqrt{2}$ | B. | $\sqrt{18}$-$\sqrt{8}$ | C. | $\sqrt{8{a}^{2}}$+$\sqrt{2a}$ | D. | $\sqrt{{x}^{2}y}$+$\sqrt{x{y}^{2}}$ |
5.下列根式中,能与$\sqrt{3}$合并的是( )
| A. | $\sqrt{12}$ | B. | $\sqrt{\frac{3}{2}}$ | C. | $\sqrt{\frac{2}{3}}$ | D. | $\sqrt{18}$ |
2.9的算术平方根是( )
| A. | -3 | B. | 3 | C. | $\frac{1}{3}$ | D. | ±3 |
1.多项式x2+5x+6与多项式x2-3x-10的公因式是( )
| A. | x+3 | B. | x-5 | C. | x-2 | D. | x+2 |
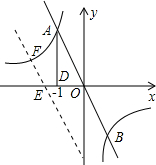 如图,反比例函数和正比例函数交于点A,B两点,A在第二象限,且点A的横坐标是-1,AD⊥x轴,垂足为D,△AOD的面积为1.
如图,反比例函数和正比例函数交于点A,B两点,A在第二象限,且点A的横坐标是-1,AD⊥x轴,垂足为D,△AOD的面积为1.