题目内容
1.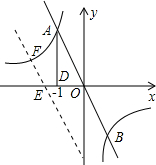 如图,反比例函数和正比例函数交于点A,B两点,A在第二象限,且点A的横坐标是-1,AD⊥x轴,垂足为D,△AOD的面积为1.
如图,反比例函数和正比例函数交于点A,B两点,A在第二象限,且点A的横坐标是-1,AD⊥x轴,垂足为D,△AOD的面积为1.(1)该反比例函数解析式为=y=-$\frac{2}{x}$;
(2)写出点B的坐标(1,-2);
(3)把直线AB向左平移1.5个单位后与x轴交于点E,与该反比例函数在第二象限的图象交于点F,求点F的坐标.
分析 (1)设反比例函数解析式为y=$\frac{k}{x}$,根据反比例系数k的几何意义结合△AOD的面积为1可得k的值;
(2)由反比例函数解析式可求得A的坐标,根据这两个函数的图象关于原点对称可得B点坐标;
(3)待定系数求直线AB解析式,进而可得平移后直线解析式,联立方程组可得交点坐标.
解答 解:(1)设反比例函数解析式为y=$\frac{k}{x}$,
∵△AOD的面积为1,
∴$\frac{1}{2}$|k|=1,
解得:k=2或k=-2,
又∵双曲线经过第二、四象限,即k<0,
∴k=-2,
∴反比例函数解析式为y=-$\frac{2}{x}$;
(2)将x=-1代入反比例函数解析式y=-$\frac{2}{x}$,得:y=2,
∴A(-1,2),
∵这两个函数的图象关于原点对称,
∴A和B这两点是关于原点对称的,
∴B点的坐标为(1,-2);
(3)设直线AB的解析式为y=ax,
将点A(-1,2)代入得:a=-2,
直线AB的解析式为y=-2x,
则向左平移1.5个单位后直线解析式为:y=-2(x+1.5)=-2x-3,
解方程组$\left\{\begin{array}{l}{y=-\frac{2}{x}}\\{y=-2x-3}\end{array}\right.$,得:$\left\{\begin{array}{l}{x=-2}\\{y=1}\end{array}\right.$,$\left\{\begin{array}{l}{x=\frac{1}{2}}\\{y=-4}\end{array}\right.$,
∴点F的坐标为(-2,1).
故答案为:(1)y=-$\frac{2}{x}$;(2)(1,-2).
点评 本题主要考查了反比例函数与一次函数的交点问题,根据反比例系数的几何意义求反比例系数与待定系数法求一次函数的解析式是关键,这里体现了数形结合的思想.

| A. | x≥$\frac{1}{2}$ | B. | x≤$\frac{1}{2}$ | C. | x≥-$\frac{1}{2}$ | D. | x≤-$\frac{1}{2}$ |
| A. | 2和3 | B. | 3和4 | C. | 4和5 | D. | 5和6 |
 由若干个相同的小立方块搭成的几何体的主视图和俯视图如图所示,这样的几何体有多少种可能的搭法?分别画出它们的左视图.
由若干个相同的小立方块搭成的几何体的主视图和俯视图如图所示,这样的几何体有多少种可能的搭法?分别画出它们的左视图. 画出下列物体的三视图.
画出下列物体的三视图.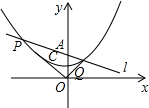 如图,O为坐标原点,直线l绕着点A(0,2)旋转,与经过点C(0,1)的抛物线y=$\frac{1}{4}$x2+h交于不同的点P,Q.求h的值.
如图,O为坐标原点,直线l绕着点A(0,2)旋转,与经过点C(0,1)的抛物线y=$\frac{1}{4}$x2+h交于不同的点P,Q.求h的值. 如图所示的是由一些相同的小正方体组成的简单几何体的主视图和俯视图,设组成这个几何体的小正方体的个数为n,则n的最大值为( )
如图所示的是由一些相同的小正方体组成的简单几何体的主视图和俯视图,设组成这个几何体的小正方体的个数为n,则n的最大值为( )