题目内容
19．当x为何值时，分式$\frac{x-2}{x+2}$的值大于0？分析 由分式的值大于0可知分式的分子和分母同号，从而得到关于x的不等式组，然后可解得x的值．
解答 解：∵分式$\frac{x-2}{x+2}$的值大于0，
∴$\left\{\begin{array}{l}{x-2＞0}\\{x+2＞0}\end{array}\right.$或$\left\{\begin{array}{l}{x-2＜0}\\{x+2＜0}\end{array}\right.$．
解得：x＞2或x＜-2．
所以当x＞2或x＜-2是分式的值大于0．
点评 本题主要考查的是分式的值，由分式的值大于0，得到关于x的不等式组是解题的关键．
练习册系列答案
字词句段篇系列答案
相关题目
14．2013年4月20日，四川省雅安市芦山县发生了7.0级大地震，给当地居民造成了巨大的损失，“一方有难，八方支援”，某市中学全体师生积极捐款，其中九年级3个班学生的捐款金额如下表：
吴老师统计时不小心把墨水滴到了其中两个班级的捐款金额上，但他知道下面两条信息：
信息一：这三个班的捐款总金额是7700元；
信息二：九（2）班的捐款金额比九（3）班的捐款金额多300元．
请根据以上信息求出九（2）班与九（3）班的捐款金额各是多少元．
| 班级 | 九（1）班 | 九（2）班 | 九（3）班 |
| 金额/元 | 2000 |
信息一：这三个班的捐款总金额是7700元；
信息二：九（2）班的捐款金额比九（3）班的捐款金额多300元．
请根据以上信息求出九（2）班与九（3）班的捐款金额各是多少元．
4．为了满足市场需求，某厂家生产A、B两种款式的布质环保购物袋，每天共生产4500个，两种购物袋的成本和售价如下表，设每天生产A种购物袋x个．
（1）每天的生产成本是多少？
（2）每天获得的利润是多少（利润=售价-成本）？（以上两问均用含x的式子表示，并将所列的式子表示进行化简）．
（3）当x=2000时，求一个月（按30天计算）的总利润是多少？
| 成本（元/个） | 售价（元/个） | |
| A | 2 | 2.3 |
| B | 3 | 3.5 |
（2）每天获得的利润是多少（利润=售价-成本）？（以上两问均用含x的式子表示，并将所列的式子表示进行化简）．
（3）当x=2000时，求一个月（按30天计算）的总利润是多少？
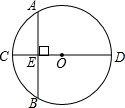已知：⊙O的半径为6cm，弦AB与直径CD垂直，且将CD分成1：3两部分，求：弦AB的长．