题目内容
2.已知A(x1,y1)、B(x2,y2)是函数y=-2x2+m(m是常数)图象上的两个点,如果x1<x2<0,那么y1,y2的大小关系是( )| A. | y1>y2 | B. | y1=y2 | ||
| C. | y1<y2 | D. | y1,y2的大小不能确定 |
分析 根据二次函数图象上点的坐标特征可求出y1=-2${{x}_{1}}^{2}$+m、y2=-2${{x}_{2}}^{2}$+m,根据x1<x2<0即可得出${{x}_{1}}^{2}$>${{x}_{2}}^{2}$,进而可得出y1<y2,此题得解.(利用二次函数的单调性更简单)
解答 解:∵A(x1,y1)、B(x2,y2)是函数y=-2x2+m(m是常数)图象上的两个点,
∴y1=-2${{x}_{1}}^{2}$+m,y2=-2${{x}_{2}}^{2}$+m,
∵x1<x2<0,
∴${{x}_{1}}^{2}$>${{x}_{2}}^{2}$,
∴y1<y2.
故选C.
(利用二次函数的单调性亦可得出y1<y2)
点评 本题考查了二次函数图象上点的坐标特征,根据二次函数图象上点的坐标特征求出y1、y2的值是解题的关键.

练习册系列答案
相关题目
17.下列函数中是反比例函数的是( )
| A. | $y=\frac{x}{3}$ | B. | $y=\frac{3}{x+1}$ | C. | $y=\frac{x^2}{2}$ | D. | $y=\frac{3}{2x}$ |
14.如果⊙O的半径为7cm,圆心O到直线l的距离为d,且d=5cm,那么⊙O和直线l的位置关系是( )
| A. | 相交 | B. | 相切 | C. | 相离 | D. | 不确定 |
2. 如图,△ABC中,∠A=65°,直线DE交AB于点D,交AC于点E,∠BDE+∠CED的值为( )
如图,△ABC中,∠A=65°,直线DE交AB于点D,交AC于点E,∠BDE+∠CED的值为( )
 如图,△ABC中,∠A=65°,直线DE交AB于点D,交AC于点E,∠BDE+∠CED的值为( )
如图,△ABC中,∠A=65°,直线DE交AB于点D,交AC于点E,∠BDE+∠CED的值为( )| A. | 180° | B. | 215° | C. | 235° | D. | 245° |
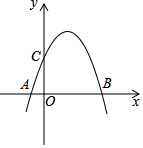 已知如图,抛物线经过点A(-1,0)、B(3,0)、C(0,2)三点,
已知如图,抛物线经过点A(-1,0)、B(3,0)、C(0,2)三点, 已知:二次函数y=ax 2+bx+c(a≠0)的图象如图所示.请你根据图象提供的信息,求出这条抛物线的表达式.
已知:二次函数y=ax 2+bx+c(a≠0)的图象如图所示.请你根据图象提供的信息,求出这条抛物线的表达式.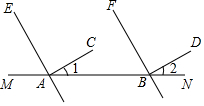 如图,AC⊥AE于A点,BD⊥BF于B点,且点A,B在直线MN上,∠1=∠2.
如图,AC⊥AE于A点,BD⊥BF于B点,且点A,B在直线MN上,∠1=∠2.